Bohr–Rogosinski radius for a certain class of close-to-convex harmonic mappings

Abstract

Let 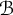$ \mathcal {B} $ be the class of analytic functions 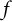$ f $ in the unit disk 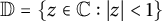$ \mathbb {D}=\{z\in \mathbb {C} : |z|<1\} $ such that 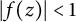$ |f(z)|<1 $ for all 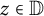$ z\in \mathbb {D} $. If 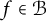$ f\in \mathcal {B} $ of the form 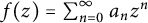$ f(z)=\sum _{n=0}^{\infty }a_nz^n $, then 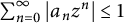$ \sum _{n=0}^{\infty }|a_nz^n|\leq 1 $ for 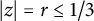$ |z|=r\leq 1/3 $ and $ 1/3 $ cannot be improved. This inequality is called Bohr inequality and the quantity 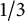$ 1/3 $ is called Bohr radius. If 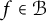$ f\in \mathcal {B} $ of the form $ f(z)=\sum _{n=0}^{\infty }a_nz^n $, then $ |\sum _{n=0}^{N}a_nz^n|<1\;\; \mbox {for}\;\; |z|<{1}/{2} $ and the radius $ 1/2 $ is the best possible for the class 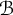$ \mathcal {B} $. This inequality is called Bohr–Rogosinski inequality and the corresponding radius is called Bohr–Rogosinski radius. Let 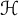$ \mathcal {H} $ be the class of all complex-valued harmonic functions 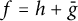$ f=h+\bar {g} $ defined on the unit disk 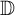$ \mathbb {D} $, where 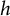$ h $ and 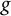$ g $ are analytic in 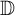$ \mathbb {D} $ with the normalization 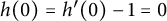$ h(0)=h^{\prime }(0)-1=0 $ and 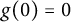$ g(0)=0 $. Let 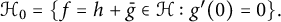$ \mathcal {H}_0=\{f=h+\bar {g}\in \mathcal {H} : g^{\prime }(0)=0\}. $ For 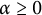$ \alpha \geq 0 $ and 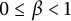$ 0\leq \beta <1 $, let

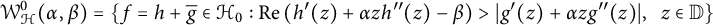$$ \begin{align*} \mathcal{W}^{0}_{\mathcal{H}}(\alpha, \beta)=\{f=h+\overline{g}\in\mathcal{H}_{0} : \mathrm{Re}\left(h^{\prime}(z)+\alpha zh^{\prime\prime}(z)-\beta\right)>|g^{\prime}(z)+\alpha zg^{\prime\prime}(z)|,\;\; z\in\mathbb{D}\} \end{align*} $$

be a class of close-to-convex harmonic mappings in 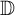$ \mathbb {D} $. In this paper, we prove the sharp Bohr–Rogosinski radius for the class 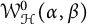$ \mathcal {W}^{0}_{\mathcal {H}}(\alpha , \beta ) $.