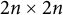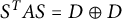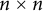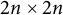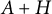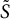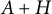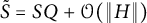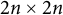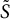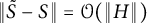1 Introduction
Analogous to the spectral theorem in linear algebra is Williamson’s theorem [Reference Williamson23] in symplectic linear algebra. It states that for any
![]() $2n \times 2n$
real positive definite matrix A, there exists a
$2n \times 2n$
real positive definite matrix A, there exists a
![]() $2n \times 2n$
real symplectic matrix S such that
$2n \times 2n$
real symplectic matrix S such that
![]() $S^TAS=D \oplus D$
, where D is an
$S^TAS=D \oplus D$
, where D is an
![]() $n\times n$
diagonal matrix with positive diagonal entries. The diagonal entries of D are known as the symplectic eigenvalues of A, and the columns of S form a symplectic eigenbasis of A. This result is also referred to as Williamson normal form in the literature [Reference DeGosson7, Reference Dutta, Mukunda and Simon8]. Symplectic eigenvalues and symplectic matrices are ubiquitous in many areas such as classical Hamiltonian dynamics [Reference Arnold2], quantum mechanics [Reference Dutta, Mukunda and Simon8], and symplectic topology [Reference Hofer and Zehnder9]. More recently, it has attracted much attention from matrix analysts [Reference Bhatia and Jain3–Reference Bhatia and Jain5, Reference Jain12–Reference Mishra14, Reference Paradan16, Reference Son and Stykel22] and quantum physicists [Reference Adesso, Serafini and Illuminati1, Reference Chen6, Reference Hsiang, Arısoy and Hu10, Reference Idel, Gaona and Wolf11, Reference Nicacio15] for its important role in continuous-variable quantum information theory [Reference Serafini19]. For example, any Gaussian state of zero mean vector is obtained by applying to a tensor product of thermal states a unitary map that is characterized by a symplectic matrix [Reference Serafini19], and the von Neumann entropy of the Gaussian state is a smooth function of the symplectic eigenvalues of its covariance matrix [Reference Parthasarathy17]. So, it is of theoretical interest as well as practical importance to study the perturbation of symplectic eigenvalues and symplectic matrices in Williamson’s theorem, both of which are closely related to each other. Indeed, the perturbation bound on symplectic eigenvalues of two positive definite matrices A and B obtained in [Reference Jain and Mishra13] is derived using symplectic matrices diagonalizing
$n\times n$
diagonal matrix with positive diagonal entries. The diagonal entries of D are known as the symplectic eigenvalues of A, and the columns of S form a symplectic eigenbasis of A. This result is also referred to as Williamson normal form in the literature [Reference DeGosson7, Reference Dutta, Mukunda and Simon8]. Symplectic eigenvalues and symplectic matrices are ubiquitous in many areas such as classical Hamiltonian dynamics [Reference Arnold2], quantum mechanics [Reference Dutta, Mukunda and Simon8], and symplectic topology [Reference Hofer and Zehnder9]. More recently, it has attracted much attention from matrix analysts [Reference Bhatia and Jain3–Reference Bhatia and Jain5, Reference Jain12–Reference Mishra14, Reference Paradan16, Reference Son and Stykel22] and quantum physicists [Reference Adesso, Serafini and Illuminati1, Reference Chen6, Reference Hsiang, Arısoy and Hu10, Reference Idel, Gaona and Wolf11, Reference Nicacio15] for its important role in continuous-variable quantum information theory [Reference Serafini19]. For example, any Gaussian state of zero mean vector is obtained by applying to a tensor product of thermal states a unitary map that is characterized by a symplectic matrix [Reference Serafini19], and the von Neumann entropy of the Gaussian state is a smooth function of the symplectic eigenvalues of its covariance matrix [Reference Parthasarathy17]. So, it is of theoretical interest as well as practical importance to study the perturbation of symplectic eigenvalues and symplectic matrices in Williamson’s theorem, both of which are closely related to each other. Indeed, the perturbation bound on symplectic eigenvalues of two positive definite matrices A and B obtained in [Reference Jain and Mishra13] is derived using symplectic matrices diagonalizing
![]() $tA+(1-t)B$
for
$tA+(1-t)B$
for
![]() $t\in [0,1]$
. In [Reference Idel, Gaona and Wolf11], a perturbation of A of the form
$t\in [0,1]$
. In [Reference Idel, Gaona and Wolf11], a perturbation of A of the form
![]() $A+tH$
was considered for small variable
$A+tH$
was considered for small variable
![]() $t> 0$
and a fixed real symmetric matrix H. The authors studied the stability of symplectic matrices diagonalizing
$t> 0$
and a fixed real symmetric matrix H. The authors studied the stability of symplectic matrices diagonalizing
![]() $A+tH$
in Williamson’s theorem and a perturbation bound was obtained for the case of A having non-repeated symplectic eigenvalues.
$A+tH$
in Williamson’s theorem and a perturbation bound was obtained for the case of A having non-repeated symplectic eigenvalues.
In this paper, we study the stability of symplectic matrices in Williamson’s theorem diagonalizing
![]() $A+H$
, where H is an arbitrary
$A+H$
, where H is an arbitrary
![]() $2n \times 2n$
real symmetric matrix such that the perturbed matrix
$2n \times 2n$
real symmetric matrix such that the perturbed matrix
![]() $A+H$
is also positive definite. Let S be a fixed symplectic matrix diagonalizing A in Williamson’s theorem. We show that any symplectic matrix
$A+H$
is also positive definite. Let S be a fixed symplectic matrix diagonalizing A in Williamson’s theorem. We show that any symplectic matrix
![]() $\tilde {S}$
diagonalizing
$\tilde {S}$
diagonalizing
![]() $A+H$
in Williamson’s theorem is of the form
$A+H$
in Williamson’s theorem is of the form
![]() $\tilde {S}=S Q+\mathcal {O}(\|H\|)$
such that Q is a
$\tilde {S}=S Q+\mathcal {O}(\|H\|)$
such that Q is a
![]() $2n \times 2n$
real symplectic as well as orthogonal matrix. Moreover, Q is in symplectic block diagonal form with block sizes given by twice the multiplicities of the symplectic eigenvalues of A. Consequently, we prove that
$2n \times 2n$
real symplectic as well as orthogonal matrix. Moreover, Q is in symplectic block diagonal form with block sizes given by twice the multiplicities of the symplectic eigenvalues of A. Consequently, we prove that
![]() $\tilde {S}$
and S can be chosen so that
$\tilde {S}$
and S can be chosen so that
![]() $\|\tilde {S}-S\|=\mathcal {O}(\|H\|)$
. Our results hold even if A has repeated symplectic eigenvalues, generalizing the stability result of symplectic matrices corresponding to the case of non-repeated symplectic eigenvalues given in [Reference Idel, Gaona and Wolf11]. We do not provide any perturbation bounds.
$\|\tilde {S}-S\|=\mathcal {O}(\|H\|)$
. Our results hold even if A has repeated symplectic eigenvalues, generalizing the stability result of symplectic matrices corresponding to the case of non-repeated symplectic eigenvalues given in [Reference Idel, Gaona and Wolf11]. We do not provide any perturbation bounds.
The rest of the paper is organized as follows: In Section 2, we review some definitions, set notations, and define basic symplectic operations. In Section 3, we detail the findings of this paper. These are given in Propositions 3.2 and 3.7 and Theorems 3.4 and 3.6.
2 Background and notations
Let
![]() $\operatorname {Sm}(m)$
denote the set of
$\operatorname {Sm}(m)$
denote the set of
![]() $m \times m$
real symmetric matrices equipped with the spectral norm
$m \times m$
real symmetric matrices equipped with the spectral norm
![]() $\|\cdot \|$
, that is, for any
$\|\cdot \|$
, that is, for any
![]() $X \in \operatorname {Sm}(m)$
,
$X \in \operatorname {Sm}(m)$
,
![]() $\|X\|$
is the maximum singular value of X. We also use the same notation
$\|X\|$
is the maximum singular value of X. We also use the same notation
![]() $\|\cdot \|$
for the Euclidean norm, and
$\|\cdot \|$
for the Euclidean norm, and
![]() $\langle \cdot , \cdot \rangle $
for the Euclidean inner product on
$\langle \cdot , \cdot \rangle $
for the Euclidean inner product on
![]() $\mathbb {R}^{m}$
or
$\mathbb {R}^{m}$
or
![]() $\mathbb {C}^m$
. Let
$\mathbb {C}^m$
. Let
![]() $0_{i,j}$
denote the
$0_{i,j}$
denote the
![]() $i \times j$
zero matrix, and let
$i \times j$
zero matrix, and let
![]() $0_i$
denote the
$0_i$
denote the
![]() $i\times i$
zero matrix (i.e.,
$i\times i$
zero matrix (i.e.,
![]() $0_i=0_{i,i}$
). We denote the imaginary unit number by
$0_i=0_{i,i}$
). We denote the imaginary unit number by
![]() . We use the Big-O notation
. We use the Big-O notation
![]() $Y=\mathcal {O}(\|X\|)$
to denote a matrix Y as a function of X for which there exist positive scalars c and
$Y=\mathcal {O}(\|X\|)$
to denote a matrix Y as a function of X for which there exist positive scalars c and
![]() $\delta $
such that
$\delta $
such that
![]() $\|Y\| \leq c \|X\|$
for all X with
$\|Y\| \leq c \|X\|$
for all X with
![]() $\|X\| < \delta $
.
$\|X\| < \delta $
.
2.1 Symplectic matrices and symplectic eigenvalues
Define
![]() , and let
, and let
![]() $J_{2n}=J_2 \otimes I_n$
for
$J_{2n}=J_2 \otimes I_n$
for
![]() $n>1$
, where
$n>1$
, where
![]() $I_n$
is the
$I_n$
is the
![]() $n \times n$
identity matrix. A
$n \times n$
identity matrix. A
![]() $2n \times 2n$
real matrix S is said to be symplectic if
$2n \times 2n$
real matrix S is said to be symplectic if
![]() $S^TJ_{2n}S=J_{2n}.$
The set of
$S^TJ_{2n}S=J_{2n}.$
The set of
![]() $2n \times 2n$
symplectic matrices, denote by
$2n \times 2n$
symplectic matrices, denote by
![]() $\operatorname {Sp}(2n)$
, forms a group under multiplication called the symplectic group. The symplectic group
$\operatorname {Sp}(2n)$
, forms a group under multiplication called the symplectic group. The symplectic group
![]() $\operatorname {Sp}(2n)$
is analogous to the orthogonal group
$\operatorname {Sp}(2n)$
is analogous to the orthogonal group
![]() $\operatorname {Or}(2n)$
of
$\operatorname {Or}(2n)$
of
![]() $2n \times 2n$
orthogonal matrices in the sense that replacing the matrix
$2n \times 2n$
orthogonal matrices in the sense that replacing the matrix
![]() $J_{2n}$
with
$J_{2n}$
with
![]() $I_{2n}$
in the definition of symplectic matrices gives the definition of orthogonal matrices. However, in contrast with the orthogonal group, the symplectic group is non-compact. Also, the determinant of every symplectic matrix is equal to
$I_{2n}$
in the definition of symplectic matrices gives the definition of orthogonal matrices. However, in contrast with the orthogonal group, the symplectic group is non-compact. Also, the determinant of every symplectic matrix is equal to
![]() $+1$
which makes the symplectic group a subgroup of the special linear group [Reference Dutta, Mukunda and Simon8]. Let
$+1$
which makes the symplectic group a subgroup of the special linear group [Reference Dutta, Mukunda and Simon8]. Let
![]() ${\operatorname {Pd}(2n) \subset \operatorname {Sm}(2n)}$
denote the set of positive definite matrices. Williamson’s theorem [Reference Williamson23] states that for every
${\operatorname {Pd}(2n) \subset \operatorname {Sm}(2n)}$
denote the set of positive definite matrices. Williamson’s theorem [Reference Williamson23] states that for every
![]() $A \in \operatorname {Pd}(2n)$
, there exists
$A \in \operatorname {Pd}(2n)$
, there exists
![]() $S\in \operatorname {Sp}(2n)$
such that
$S\in \operatorname {Sp}(2n)$
such that
![]() $S^TAS=D \oplus D$
, where D is an
$S^TAS=D \oplus D$
, where D is an
![]() $n\times n$
diagonal matrix. The diagonal elements
$n\times n$
diagonal matrix. The diagonal elements
![]() $d_1(A) \le \cdots \le d_n(A)$
of D are independent of the choice of S, and they are known as the symplectic eigenvalues of A. Denote by
$d_1(A) \le \cdots \le d_n(A)$
of D are independent of the choice of S, and they are known as the symplectic eigenvalues of A. Denote by
![]() $\operatorname {Sp}(2n; A)$
the subset of
$\operatorname {Sp}(2n; A)$
the subset of
![]() $\operatorname {Sp}(2n)$
consisting of symplectic matrices that diagonalize A in Williamson’s theorem. Several proofs of Williamson’s theorem are available using basic linear algebra (e.g., [Reference DeGosson7, Reference Simon, Chaturvedi and Srinivasan20]).
$\operatorname {Sp}(2n)$
consisting of symplectic matrices that diagonalize A in Williamson’s theorem. Several proofs of Williamson’s theorem are available using basic linear algebra (e.g., [Reference DeGosson7, Reference Simon, Chaturvedi and Srinivasan20]).
Denote the set of
![]() $2n \times 2n$
orthosymplectic (orthogonal as well as symplectic) matrices as
$2n \times 2n$
orthosymplectic (orthogonal as well as symplectic) matrices as
![]() . Any orthosymplectic matrix
. Any orthosymplectic matrix
![]() $Q \in \operatorname {OrSp}(2n)$
is precisely of the form
$Q \in \operatorname {OrSp}(2n)$
is precisely of the form
 $$ \begin{align} Q = \begin{pmatrix} X & Y \\ -Y & X \end{pmatrix}, \end{align} $$
$$ \begin{align} Q = \begin{pmatrix} X & Y \\ -Y & X \end{pmatrix}, \end{align} $$
where
![]() $X,Y$
are
$X,Y$
are
![]() $n\times n$
real matrices such that
$n\times n$
real matrices such that
![]() $X+\iota Y$
is a unitary matrix [Reference Bhatia and Jain3]. For
$X+\iota Y$
is a unitary matrix [Reference Bhatia and Jain3]. For
![]() $m \leq n$
, we denote by
$m \leq n$
, we denote by
![]() $\operatorname {Sp}(2n, 2m)$
the set of
$\operatorname {Sp}(2n, 2m)$
the set of
![]() $2n \times 2m$
matrices M satisfying
$2n \times 2m$
matrices M satisfying
![]() $M^T J_{2n} M = J_{2m}$
. In particular, we have
$M^T J_{2n} M = J_{2m}$
. In particular, we have
![]() $\operatorname {Sp}(2n, 2n)=\operatorname {Sp}(2n)$
.
$\operatorname {Sp}(2n, 2n)=\operatorname {Sp}(2n)$
.
2.2 Symplectic block and symplectic direct sum
Let m be a natural number and
![]() $\mathcal {I}, \mathcal {J} \subseteq \{1, \ldots , m\}$
. Suppose M is an
$\mathcal {I}, \mathcal {J} \subseteq \{1, \ldots , m\}$
. Suppose M is an
![]() $m\times m$
matrix. We denote by
$m\times m$
matrix. We denote by
![]() $M_{\mathcal {J}}$
the submatrix of M consisting of the columns of M with indices in
$M_{\mathcal {J}}$
the submatrix of M consisting of the columns of M with indices in
![]() $\mathcal {J}$
. Also, denote by
$\mathcal {J}$
. Also, denote by
![]() $M_{\mathcal {I} \mathcal {J}}$
the
$M_{\mathcal {I} \mathcal {J}}$
the
![]() $|\mathcal {I}| \times |\mathcal {J}|$
submatrix of
$|\mathcal {I}| \times |\mathcal {J}|$
submatrix of
![]() $M=[M_{ij}]$
consisting of the elements
$M=[M_{ij}]$
consisting of the elements
![]() $M_{ij}$
with indices
$M_{ij}$
with indices
![]() $i\in \mathcal {I}$
and
$i\in \mathcal {I}$
and
![]() $j\in \mathcal {J}$
. Let T be any
$j\in \mathcal {J}$
. Let T be any
![]() $2m \times 2m$
matrix given in the block form by
$2m \times 2m$
matrix given in the block form by
 $$ \begin{align*} T = \begin{pmatrix} W & X \\ Y & Z \end{pmatrix}, \end{align*} $$
$$ \begin{align*} T = \begin{pmatrix} W & X \\ Y & Z \end{pmatrix}, \end{align*} $$
where
![]() $X,Y,W,Z$
are matrices of order
$X,Y,W,Z$
are matrices of order
![]() $m \times m$
. Define a symplectic block of T as a submatrix of the form
$m \times m$
. Define a symplectic block of T as a submatrix of the form
 $$ \begin{align*} \begin{pmatrix} W_{\mathcal{I}\mathcal{J}} & X_{\mathcal{I}\mathcal{J}} \\ Y_{\mathcal{I}\mathcal{J}} & Z_{\mathcal{I}\mathcal{J}} \end{pmatrix}. \end{align*} $$
$$ \begin{align*} \begin{pmatrix} W_{\mathcal{I}\mathcal{J}} & X_{\mathcal{I}\mathcal{J}} \\ Y_{\mathcal{I}\mathcal{J}} & Z_{\mathcal{I}\mathcal{J}} \end{pmatrix}. \end{align*} $$
Also, define a symplectic diagonal block of T as a submatrix of the form
 $$ \begin{align*} \begin{pmatrix} W_{\mathcal{I}\mathcal{I}} & X_{\mathcal{I}\mathcal{I}} \\ Y_{\mathcal{I}\mathcal{I}} & Z_{\mathcal{I}\mathcal{I}} \end{pmatrix}. \end{align*} $$
$$ \begin{align*} \begin{pmatrix} W_{\mathcal{I}\mathcal{I}} & X_{\mathcal{I}\mathcal{I}} \\ Y_{\mathcal{I}\mathcal{I}} & Z_{\mathcal{I}\mathcal{I}} \end{pmatrix}. \end{align*} $$
The following example illustrates this.
Example 2.1 Let T be a
![]() $6 \times 6$
matrix given by
$6 \times 6$
matrix given by

A symplectic block of T, which corresponds to
![]() $\mathcal {I}=\{3\}$
and
$\mathcal {I}=\{3\}$
and
![]() $\mathcal {J}=\{2\}$
, is given by
$\mathcal {J}=\{2\}$
, is given by

A symplectic diagonal block, corresponding to
![]() $\mathcal {I}=\{1,2\}$
, is given by
$\mathcal {I}=\{1,2\}$
, is given by

Let
![]() $T'$
be another
$T'$
be another
![]() $2m' \times 2m'$
matrix, given in the block form
$2m' \times 2m'$
matrix, given in the block form
 $$ \begin{align*} T' = \begin{pmatrix} W' & X' \\ Y' & Z' \end{pmatrix}, \end{align*} $$
$$ \begin{align*} T' = \begin{pmatrix} W' & X' \\ Y' & Z' \end{pmatrix}, \end{align*} $$
where the blocks
![]() $W',X',Y',Z'$
have size
$W',X',Y',Z'$
have size
![]() $m' \times m'$
. Define the symplectic direct sum of T and
$m' \times m'$
. Define the symplectic direct sum of T and
![]() $T'$
as
$T'$
as
 $$ \begin{align*} T \oplus^{\operatorname{s}} T' &= \begin{pmatrix} W \oplus W' & X \oplus X' \\ Y \oplus Y' & Z \oplus Z' \end{pmatrix}. \end{align*} $$
$$ \begin{align*} T \oplus^{\operatorname{s}} T' &= \begin{pmatrix} W \oplus W' & X \oplus X' \\ Y \oplus Y' & Z \oplus Z' \end{pmatrix}. \end{align*} $$
This is illustrated in the following example.
Example 2.2 Let

We then have

We know that the usual direct sum of two orthogonal matrices is also an orthogonal matrix. It is interesting to note that an analogous property is also satisfied by the symplectic direct sum. If
![]() $T \in \operatorname {Sp}(2k)$
and
$T \in \operatorname {Sp}(2k)$
and
![]() $T' \in \operatorname {Sp}(2\ell )$
, then
$T' \in \operatorname {Sp}(2\ell )$
, then
![]() $T \oplus ^s T' \in \operatorname {Sp}(2(k+\ell ))$
. Indeed, we have
$T \oplus ^s T' \in \operatorname {Sp}(2(k+\ell ))$
. Indeed, we have
 $$ \begin{align*} &(T \oplus^s T')^T J_{2(k+\ell)} (T \oplus^s T') \\[3pt] &\hspace{0.5cm}= \begin{pmatrix} W \oplus W' & X \oplus X' \\ Y \oplus Y' & Z \oplus Z' \end{pmatrix}^T \begin{pmatrix} 0_{k+\ell} & I_{k+\ell} \\ -I_{k+\ell} & 0_{k+\ell} \end{pmatrix} \begin{pmatrix} W \oplus W' & X \oplus X' \\ Y \oplus Y' & Z \oplus Z' \end{pmatrix} \\[3pt] &\hspace{0.5cm}= \begin{pmatrix} W^T \oplus W'^T & Y^T \oplus Y'^T \\ X^T \oplus X'^T & Z^T \oplus Z'^T \end{pmatrix} \begin{pmatrix} Y \oplus Y' & Z \oplus Z' \\ -(W \oplus W') & -(X \oplus X') \end{pmatrix} \\[3pt] &\hspace{0.5cm}= \begin{pmatrix} W^TY \oplus W'^TY' - Y^TW \oplus Y'^TW' & W^TZ \oplus W'^TZ' - Y^TX \oplus Y'^TX' \\ X^TY \oplus X'^TY'- Z^TW \oplus Z'^TW' & X^TZ \oplus X'^TZ' - Z^TX \oplus Z'^TX' \end{pmatrix} \\[3pt] &\hspace{0.5cm}= \begin{pmatrix} (W^TY- Y^TW) \oplus (W'^TY' - Y'^TW') & \!\!\!\!\!(W^TZ- Y^TX) \oplus (W'^TZ'- Y'^TX') \\ (X^TY- Z^TW) \oplus (X'^TY' - Z'^TW') &\!\!\!\!\! (X^TZ- Z^TX) \oplus (X'^TZ' - Z'^TX') \end{pmatrix} \\[3pt] &\hspace{0.5cm}= \begin{pmatrix} W^TY- Y^TW & W^TZ- Y^TX \\ X^TY- Z^TW & X^TZ- Z^TX \end{pmatrix} \oplus^s \begin{pmatrix} W'^TY' - Y'^TW' & W'^TZ'- Y'^TX' \\ X'^TY' - Z'^TW' & X'^TZ' - Z'^TX' \end{pmatrix} \\[3pt] &\hspace{0.5cm}= \begin{pmatrix} W^T & Y^T \\ X^T & Z^T \end{pmatrix} \begin{pmatrix} Y & Z \\ -W & -X \end{pmatrix} \oplus^s \begin{pmatrix} W'^T & Y'^T \\ X'^T & Z'^T \end{pmatrix} \begin{pmatrix} Y' & Z' \\ -W' & -X' \end{pmatrix} \\[3pt] &\hspace{0.5cm}= \begin{pmatrix} W & X \\ Y & Z \end{pmatrix}^T \begin{pmatrix} 0_k & I_k \\ -I_k & 0_k \end{pmatrix} \begin{pmatrix} W & X \\ Y & Z \end{pmatrix} \oplus^s \begin{pmatrix} W' & X' \\ Y' & Z' \end{pmatrix}^T \begin{pmatrix} 0_{\ell} & I_\ell \\ -I_\ell & 0_{\ell} \end{pmatrix} \begin{pmatrix} W' & X' \\ Y' & Z' \end{pmatrix} \\[3pt] &\hspace{0.5cm}= T^T J_{2k}T \oplus^s T'^T J_{2\ell} T' \\[3pt] &\hspace{0.5cm}= J_{2k} \oplus^s J_{2\ell} \\[3pt] &\hspace{0.5cm}= J_{2(k+\ell)}.\end{align*} $$
$$ \begin{align*} &(T \oplus^s T')^T J_{2(k+\ell)} (T \oplus^s T') \\[3pt] &\hspace{0.5cm}= \begin{pmatrix} W \oplus W' & X \oplus X' \\ Y \oplus Y' & Z \oplus Z' \end{pmatrix}^T \begin{pmatrix} 0_{k+\ell} & I_{k+\ell} \\ -I_{k+\ell} & 0_{k+\ell} \end{pmatrix} \begin{pmatrix} W \oplus W' & X \oplus X' \\ Y \oplus Y' & Z \oplus Z' \end{pmatrix} \\[3pt] &\hspace{0.5cm}= \begin{pmatrix} W^T \oplus W'^T & Y^T \oplus Y'^T \\ X^T \oplus X'^T & Z^T \oplus Z'^T \end{pmatrix} \begin{pmatrix} Y \oplus Y' & Z \oplus Z' \\ -(W \oplus W') & -(X \oplus X') \end{pmatrix} \\[3pt] &\hspace{0.5cm}= \begin{pmatrix} W^TY \oplus W'^TY' - Y^TW \oplus Y'^TW' & W^TZ \oplus W'^TZ' - Y^TX \oplus Y'^TX' \\ X^TY \oplus X'^TY'- Z^TW \oplus Z'^TW' & X^TZ \oplus X'^TZ' - Z^TX \oplus Z'^TX' \end{pmatrix} \\[3pt] &\hspace{0.5cm}= \begin{pmatrix} (W^TY- Y^TW) \oplus (W'^TY' - Y'^TW') & \!\!\!\!\!(W^TZ- Y^TX) \oplus (W'^TZ'- Y'^TX') \\ (X^TY- Z^TW) \oplus (X'^TY' - Z'^TW') &\!\!\!\!\! (X^TZ- Z^TX) \oplus (X'^TZ' - Z'^TX') \end{pmatrix} \\[3pt] &\hspace{0.5cm}= \begin{pmatrix} W^TY- Y^TW & W^TZ- Y^TX \\ X^TY- Z^TW & X^TZ- Z^TX \end{pmatrix} \oplus^s \begin{pmatrix} W'^TY' - Y'^TW' & W'^TZ'- Y'^TX' \\ X'^TY' - Z'^TW' & X'^TZ' - Z'^TX' \end{pmatrix} \\[3pt] &\hspace{0.5cm}= \begin{pmatrix} W^T & Y^T \\ X^T & Z^T \end{pmatrix} \begin{pmatrix} Y & Z \\ -W & -X \end{pmatrix} \oplus^s \begin{pmatrix} W'^T & Y'^T \\ X'^T & Z'^T \end{pmatrix} \begin{pmatrix} Y' & Z' \\ -W' & -X' \end{pmatrix} \\[3pt] &\hspace{0.5cm}= \begin{pmatrix} W & X \\ Y & Z \end{pmatrix}^T \begin{pmatrix} 0_k & I_k \\ -I_k & 0_k \end{pmatrix} \begin{pmatrix} W & X \\ Y & Z \end{pmatrix} \oplus^s \begin{pmatrix} W' & X' \\ Y' & Z' \end{pmatrix}^T \begin{pmatrix} 0_{\ell} & I_\ell \\ -I_\ell & 0_{\ell} \end{pmatrix} \begin{pmatrix} W' & X' \\ Y' & Z' \end{pmatrix} \\[3pt] &\hspace{0.5cm}= T^T J_{2k}T \oplus^s T'^T J_{2\ell} T' \\[3pt] &\hspace{0.5cm}= J_{2k} \oplus^s J_{2\ell} \\[3pt] &\hspace{0.5cm}= J_{2(k+\ell)}.\end{align*} $$
2.3 Symplectic concatenation
Let
![]() $M=\left (p_1,\ldots , p_{k}, q_1,\ldots ,q_k \right )$
and
$M=\left (p_1,\ldots , p_{k}, q_1,\ldots ,q_k \right )$
and
![]() $N=\left (x_1,\ldots , x_{\ell }, y_1,\ldots ,y_\ell \right )$
be
$N=\left (x_1,\ldots , x_{\ell }, y_1,\ldots ,y_\ell \right )$
be
![]() $2n \times 2k$
and
$2n \times 2k$
and
![]() ${2n \times 2\ell }$
matrices, respectively. Define the symplectic concatenation of M and N to be the following
${2n \times 2\ell }$
matrices, respectively. Define the symplectic concatenation of M and N to be the following
![]() $2n \times 2(k+\ell )$
matrix:
$2n \times 2(k+\ell )$
matrix:
Here is an example to illustrate symplectic concatenation.
Example 2.3 Let

The symplectic concatenation of M and N is given by

Suppose that
![]() $M \in \operatorname {Sp}(2n, 2k)$
and
$M \in \operatorname {Sp}(2n, 2k)$
and
![]() $N \in \operatorname {Sp}(2n, 2\ell )$
. Let us derive a necessary and sufficient condition on M and N for
$N \in \operatorname {Sp}(2n, 2\ell )$
. Let us derive a necessary and sufficient condition on M and N for
![]() $k+\ell \leq n$
such that
$k+\ell \leq n$
such that
![]() $M \diamond N \in \operatorname {Sp}(2n, 2(k+\ell ))$
. This will be useful later. We have
$M \diamond N \in \operatorname {Sp}(2n, 2(k+\ell ))$
. This will be useful later. We have
 $$ \begin{align} (M \diamond N)^T J_{2n} (M \diamond N) &= \left((M \diamond N)^T J_{2n} M \right) \diamond \left((M \diamond N)^T J_{2n}N\right) \nonumber \\ &=\left(M^T J_{2n}^T (M \diamond N) \right)^T \diamond \left(N^TJ_{2n}^T(M \diamond N)\right)^T \nonumber \\ &=\left((M^T J_{2n}^T M) \diamond (M^T J_{2n}^T N) \right)^T \diamond \left((N^TJ_{2n}^TM) \diamond (N^TJ_{2n}^TN)\right)^T \nonumber \\ &= \left(J_{2k}^T \diamond (M^T J_{2n}^T N) \right)^T \diamond \left((N^TJ_{2n}^TM) \diamond J_{2\ell}^T\right)^T. \end{align} $$
$$ \begin{align} (M \diamond N)^T J_{2n} (M \diamond N) &= \left((M \diamond N)^T J_{2n} M \right) \diamond \left((M \diamond N)^T J_{2n}N\right) \nonumber \\ &=\left(M^T J_{2n}^T (M \diamond N) \right)^T \diamond \left(N^TJ_{2n}^T(M \diamond N)\right)^T \nonumber \\ &=\left((M^T J_{2n}^T M) \diamond (M^T J_{2n}^T N) \right)^T \diamond \left((N^TJ_{2n}^TM) \diamond (N^TJ_{2n}^TN)\right)^T \nonumber \\ &= \left(J_{2k}^T \diamond (M^T J_{2n}^T N) \right)^T \diamond \left((N^TJ_{2n}^TM) \diamond J_{2\ell}^T\right)^T. \end{align} $$
We also observe that
By comparing (2.2) and (2.3), we deduce that
![]() $M \diamond N \in \operatorname {Sp}(2n, 2(k+\ell ))$
if and only if
$M \diamond N \in \operatorname {Sp}(2n, 2(k+\ell ))$
if and only if
![]() $M^T J_{2n} N=0_{2k, 2\ell }$
.
$M^T J_{2n} N=0_{2k, 2\ell }$
.
3 Main results
We fix the following notations throughout the paper. Let
![]() $A \in \operatorname {Pd}(2n)$
with distinct symplectic eigenvalues
$A \in \operatorname {Pd}(2n)$
with distinct symplectic eigenvalues
![]() $\mu _1 < \cdots < \mu _r$
. For all
$\mu _1 < \cdots < \mu _r$
. For all
![]() $i=1, \ldots , r$
, define sets
$i=1, \ldots , r$
, define sets

An example to illustrate these sets is as follows.
Example 3.1 Suppose
![]() $A \in \operatorname {Pd}(20)$
with symplectic eigenvalues
$A \in \operatorname {Pd}(20)$
with symplectic eigenvalues
![]() $1,1,2,3,3,3,4,4,4,5$
. We have
$1,1,2,3,3,3,4,4,4,5$
. We have
![]() $\mu _1=1,\ \mu _2=2,\ \mu _3=3,\ \mu _4=4,\ \mu _5=5$
. Also
$\mu _1=1,\ \mu _2=2,\ \mu _3=3,\ \mu _4=4,\ \mu _5=5$
. Also
![]() $\alpha _1=\{1,2\}$
,
$\alpha _1=\{1,2\}$
,
![]() $\alpha _2=\{3\}, \alpha _3=\{4,5,6\}, \alpha _4=\{7,8,9\}, \alpha _5=\{10\}$
. Note that
$\alpha _2=\{3\}, \alpha _3=\{4,5,6\}, \alpha _4=\{7,8,9\}, \alpha _5=\{10\}$
. Note that
![]() $n=10$
, so we have
$n=10$
, so we have
![]() $\beta _1=\{11,12\}$
,
$\beta _1=\{11,12\}$
,
![]() $\beta _2=\{13\}, \beta _3=\{14,15,16\}$
,
$\beta _2=\{13\}, \beta _3=\{14,15,16\}$
,
![]() $\beta _4=\{17,18,19\}$
,
$\beta _4=\{17,18,19\}$
,
![]() $\beta _5=\{20\}$
. We thus also get
$\beta _5=\{20\}$
. We thus also get
![]() $\gamma _1=\{1,2,11,12\}$
,
$\gamma _1=\{1,2,11,12\}$
,
![]() $\gamma _2=\{3,13\}$
,
$\gamma _2=\{3,13\}$
,
![]() $\gamma _3=\{4,5,6,14,15,16\}$
,
$\gamma _3=\{4,5,6,14,15,16\}$
,
![]() $\gamma _4=\{7,8,9,17,18,19\}$
,
$\gamma _4=\{7,8,9,17,18,19\}$
,
![]() $\gamma _5=\{10,20\}$
.
$\gamma _5=\{10,20\}$
.
Proposition 3.2 Let
![]() $A \in \operatorname {Pd}(2n)$
and
$A \in \operatorname {Pd}(2n)$
and
![]() $H\in \operatorname {Sm}(2n)$
such that
$H\in \operatorname {Sm}(2n)$
such that
![]() $A + H \in \operatorname {Pd}(2n).$
Let
$A + H \in \operatorname {Pd}(2n).$
Let
![]() ${S\in \operatorname {Sp}(2n; A)}$
and
${S\in \operatorname {Sp}(2n; A)}$
and
![]() $\tilde {S} \in \operatorname {Sp}(2n; A+H)$
. For
$\tilde {S} \in \operatorname {Sp}(2n; A+H)$
. For
![]() $1\leq i\neq j\leq r$
, we have
$1\leq i\neq j\leq r$
, we have
Proof It suffices to prove the assertions for A in the diagonal form
![]() $A=D \oplus D$
and
$A=D \oplus D$
and
![]() $S=I_{2n}$
. For any
$S=I_{2n}$
. For any
![]() $\tilde {S} \in \operatorname {Sp}(2n; A+H)$
, we have
$\tilde {S} \in \operatorname {Sp}(2n; A+H)$
, we have
where
![]() $\tilde {D}$
is the diagonal matrix with entries
$\tilde {D}$
is the diagonal matrix with entries
![]() $d_1(A+H) \leq \cdots \leq d_n(A+H)$
. By Theorem
$d_1(A+H) \leq \cdots \leq d_n(A+H)$
. By Theorem
![]() $3.1$
of [Reference Idel, Gaona and Wolf11], we get
$3.1$
of [Reference Idel, Gaona and Wolf11], we get
By (3.6) and (3.7), and using the diagonal form
![]() $A=D \oplus D$
, we get
$A=D \oplus D$
, we get
The symplectic matrix
![]() $\tilde {S}$
satisfies
$\tilde {S}$
satisfies
 $$ \begin{align*} \|\tilde{S}\|^2 &= \|(A+H)^{-1/2}(A+H)^{1/2}\tilde{S} \|^2 \\ &\leq \|(A+H)^{-1/2}\|^2 \|(A+H)^{1/2}\tilde{S} \|^2 \\ &= \|(A+H)^{-1}\| \| \tilde{S}^T(A+H)\tilde{S} \|\\ &=2\|(A+H)^{-1}\| d_{1}(A+H)\\ &\leq 2\|(A+H)^{-1}\| \|A+H\| = 2\kappa(A+H), \end{align*} $$
$$ \begin{align*} \|\tilde{S}\|^2 &= \|(A+H)^{-1/2}(A+H)^{1/2}\tilde{S} \|^2 \\ &\leq \|(A+H)^{-1/2}\|^2 \|(A+H)^{1/2}\tilde{S} \|^2 \\ &= \|(A+H)^{-1}\| \| \tilde{S}^T(A+H)\tilde{S} \|\\ &=2\|(A+H)^{-1}\| d_{1}(A+H)\\ &\leq 2\|(A+H)^{-1}\| \|A+H\| = 2\kappa(A+H), \end{align*} $$
where
![]() $\kappa (T)=\|T\|\|T^{-1}\|$
is the condition number of an invertible matrix T, and we used [Reference Jain and Mishra13, Lemma 2.2(iii)] in the last inequality. It thus implies that
$\kappa (T)=\|T\|\|T^{-1}\|$
is the condition number of an invertible matrix T, and we used [Reference Jain and Mishra13, Lemma 2.2(iii)] in the last inequality. It thus implies that
![]() $\|\tilde {S}\|$
is uniformly bounded for small
$\|\tilde {S}\|$
is uniformly bounded for small
![]() $\|H\|$
, which follows from the continuity of
$\|H\|$
, which follows from the continuity of
![]() $\kappa $
. So, from (3.8) and the symplectic relation
$\kappa $
. So, from (3.8) and the symplectic relation
![]() $\tilde {S}^{-T}=J_{2n}\tilde {S}J_{2n}^T$
, we get
$\tilde {S}^{-T}=J_{2n}\tilde {S}J_{2n}^T$
, we get
Consider
![]() $\tilde {S}$
in the block matrix form:
$\tilde {S}$
in the block matrix form:
 $$ \begin{align*} \tilde{S}= \begin{pmatrix} \tilde{W} & \tilde{X} \\ \tilde{Y} & \tilde{Z} \end{pmatrix}, \end{align*} $$
$$ \begin{align*} \tilde{S}= \begin{pmatrix} \tilde{W} & \tilde{X} \\ \tilde{Y} & \tilde{Z} \end{pmatrix}, \end{align*} $$
where each block
![]() $\tilde {W}, \tilde {X}, \tilde {Y}, \tilde {Z}$
has size
$\tilde {W}, \tilde {X}, \tilde {Y}, \tilde {Z}$
has size
![]() $n \times n$
. From (3.9) and using the fact
$n \times n$
. From (3.9) and using the fact
![]() $A=D \oplus D$
, we get
$A=D \oplus D$
, we get
 $$ \begin{align} \begin{pmatrix} D\tilde{W} & D\tilde{X} \\ D\tilde{Y} & D\tilde{Z} \end{pmatrix} &= \begin{pmatrix} 0_n & I_n \\ -I_n & 0_n \end{pmatrix} \begin{pmatrix} \tilde{W} & \tilde{X} \\ \tilde{Y} & \tilde{Z} \end{pmatrix} \begin{pmatrix} 0_n & -I_n \\ I_n & 0_n \end{pmatrix} \begin{pmatrix} D & 0_n \\ 0_n & D \end{pmatrix} + \mathcal{O}(\|H\|) \nonumber \\ &= \begin{pmatrix} \tilde{Z}D & -\tilde{Y}D \\ -\tilde{X}D & \tilde{W}D \end{pmatrix} + \mathcal{O}(\|H\|). \end{align} $$
$$ \begin{align} \begin{pmatrix} D\tilde{W} & D\tilde{X} \\ D\tilde{Y} & D\tilde{Z} \end{pmatrix} &= \begin{pmatrix} 0_n & I_n \\ -I_n & 0_n \end{pmatrix} \begin{pmatrix} \tilde{W} & \tilde{X} \\ \tilde{Y} & \tilde{Z} \end{pmatrix} \begin{pmatrix} 0_n & -I_n \\ I_n & 0_n \end{pmatrix} \begin{pmatrix} D & 0_n \\ 0_n & D \end{pmatrix} + \mathcal{O}(\|H\|) \nonumber \\ &= \begin{pmatrix} \tilde{Z}D & -\tilde{Y}D \\ -\tilde{X}D & \tilde{W}D \end{pmatrix} + \mathcal{O}(\|H\|). \end{align} $$
Now, using the representation
![]() $D = \mu _1 I_{|\alpha _1|} \oplus \cdots \oplus \mu _r I_{|\alpha _r|}$
, and comparing the corresponding blocks on both sides in (3.10), we get, for all
$D = \mu _1 I_{|\alpha _1|} \oplus \cdots \oplus \mu _r I_{|\alpha _r|}$
, and comparing the corresponding blocks on both sides in (3.10), we get, for all
![]() $1 \leq i,j \leq r$
,
$1 \leq i,j \leq r$
,
 $$ \begin{align} \begin{pmatrix} \mu_i \tilde{W}_{\alpha_i \alpha_j} & \mu_i \tilde{X}_{\alpha_i \alpha_j} \\ \mu_i \tilde{Y}_{\alpha_i \alpha_j} & \mu_i \tilde{Z}_{\alpha_i \alpha_j} \end{pmatrix} &= \begin{pmatrix} \mu_j \tilde{Z}_{\alpha_i \alpha_j} & -\mu_j \tilde{Y}_{\alpha_i \alpha_j} \\ -\mu_j \tilde{X}_{\alpha_i \alpha_j} & \mu_j \tilde{W}_{\alpha_i \alpha_j} \end{pmatrix} + \mathcal{O}(\|H\|). \end{align} $$
$$ \begin{align} \begin{pmatrix} \mu_i \tilde{W}_{\alpha_i \alpha_j} & \mu_i \tilde{X}_{\alpha_i \alpha_j} \\ \mu_i \tilde{Y}_{\alpha_i \alpha_j} & \mu_i \tilde{Z}_{\alpha_i \alpha_j} \end{pmatrix} &= \begin{pmatrix} \mu_j \tilde{Z}_{\alpha_i \alpha_j} & -\mu_j \tilde{Y}_{\alpha_i \alpha_j} \\ -\mu_j \tilde{X}_{\alpha_i \alpha_j} & \mu_j \tilde{W}_{\alpha_i \alpha_j} \end{pmatrix} + \mathcal{O}(\|H\|). \end{align} $$
This can be equivalently represented as
This also gives
Adding (3.12) and (3.13), and then dividing by
![]() $\mu _i+\mu _j$
, gives
$\mu _i+\mu _j$
, gives
Suppose, we have
![]() $i\neq j$
. This implies
$i\neq j$
. This implies
![]() $\mu _i \neq \mu _j.$
By subtracting (3.13) from (3.12), and then dividing by
$\mu _i \neq \mu _j.$
By subtracting (3.13) from (3.12), and then dividing by
![]() $\mu _i-\mu _j$
, we then get
$\mu _i-\mu _j$
, we then get
By adding (3.14) and (3.15), we get
![]() $\tilde {S}_{\gamma _i \gamma _j}=\mathcal {O}(\|H\|)$
. This settles (3.1).
$\tilde {S}_{\gamma _i \gamma _j}=\mathcal {O}(\|H\|)$
. This settles (3.1).
We get (3.2) and (3.3) directly as a consequence of (3.11) by taking
![]() $i=j$
.
$i=j$
.
By the symplectic relation
![]() $\tilde {S}^TJ_{2n}\tilde {S}=J_{2n},$
we get
$\tilde {S}^TJ_{2n}\tilde {S}=J_{2n},$
we get
 $$ \begin{align} J_{2|\alpha_i|} &= \tilde{S}^T_{\gamma_i}J_{2n}\tilde{S}_{\gamma_i} \nonumber \\ &= \sum_{k=1}^r \tilde{S}_{\gamma_k\gamma_i}^T J_{2|\alpha_k|} \tilde{S}_{\gamma_k\gamma_i} \nonumber \\ &= \tilde{S}_{\gamma_i\gamma_i}^T J_{2|\alpha_i|} \tilde{S}_{\gamma_i\gamma_i} + \sum_{k\neq i, k=1}^r \tilde{S}_{\gamma_k\gamma_i}^T J_{2|\alpha_k|} \tilde{S}_{\gamma_k\gamma_i}. \end{align} $$
$$ \begin{align} J_{2|\alpha_i|} &= \tilde{S}^T_{\gamma_i}J_{2n}\tilde{S}_{\gamma_i} \nonumber \\ &= \sum_{k=1}^r \tilde{S}_{\gamma_k\gamma_i}^T J_{2|\alpha_k|} \tilde{S}_{\gamma_k\gamma_i} \nonumber \\ &= \tilde{S}_{\gamma_i\gamma_i}^T J_{2|\alpha_i|} \tilde{S}_{\gamma_i\gamma_i} + \sum_{k\neq i, k=1}^r \tilde{S}_{\gamma_k\gamma_i}^T J_{2|\alpha_k|} \tilde{S}_{\gamma_k\gamma_i}. \end{align} $$
We know by (3.1) that
![]() $\tilde {S}_{\gamma _k\gamma _i} = \mathcal {O}(\|H\|)$
for all
$\tilde {S}_{\gamma _k\gamma _i} = \mathcal {O}(\|H\|)$
for all
![]() $k \neq i$
. Using this in the second term of (3.16), we get
$k \neq i$
. Using this in the second term of (3.16), we get
This implies (3.5). The relation (3.17) also gives
The two relations (3.2) and (3.3) can be combined and expressed as
Substituting (3.19) in (3.18) gives
This proves the remaining assertion (3.4).
Remark 3.3 By taking
![]() $H=0_{2n,2n}$
in Proposition 3.2, we observe that
$H=0_{2n,2n}$
in Proposition 3.2, we observe that
![]() $\left (S^{-1}\tilde {S}\right )_{\gamma _i \gamma _j}=0_{2|\alpha _i|, 2|\alpha _j|}$
for
$\left (S^{-1}\tilde {S}\right )_{\gamma _i \gamma _j}=0_{2|\alpha _i|, 2|\alpha _j|}$
for
![]() $i\neq j$
, and that
$i\neq j$
, and that
![]() is orthosymplectic for all i. This implies
is orthosymplectic for all i. This implies
![]() $\tilde {S}=S Q$
, where
$\tilde {S}=S Q$
, where
![]() $Q=Q_{[1]} \oplus ^{\operatorname {s}} \cdots \oplus ^{\operatorname {s}} Q_{[r]}$
is orthosymplectic. The following result generalizes this observation for arbitrary
$Q=Q_{[1]} \oplus ^{\operatorname {s}} \cdots \oplus ^{\operatorname {s}} Q_{[r]}$
is orthosymplectic. The following result generalizes this observation for arbitrary
![]() $H \to 0_{2n}$
.
$H \to 0_{2n}$
.
Theorem 3.4 Let
![]() $A \in \operatorname {Pd}(2n)$
and
$A \in \operatorname {Pd}(2n)$
and
![]() $H\in \operatorname {Sm}(2n)$
such that
$H\in \operatorname {Sm}(2n)$
such that
![]() $A + H \in \operatorname {Pd}(2n).$
Let
$A + H \in \operatorname {Pd}(2n).$
Let
![]() ${S\in \operatorname {Sp}(2n; A)}$
and
${S\in \operatorname {Sp}(2n; A)}$
and
![]() $\tilde {S} \in \operatorname {Sp}(2n; A+H)$
be arbitrary. Then, there exists an orthosymplectic matrix Q of the form
$\tilde {S} \in \operatorname {Sp}(2n; A+H)$
be arbitrary. Then, there exists an orthosymplectic matrix Q of the form
where
![]() $Q_{[i]} \in \operatorname {OrSp}(2|\alpha _i|)$
for all
$Q_{[i]} \in \operatorname {OrSp}(2|\alpha _i|)$
for all
![]() $i=1,\ldots ,r$
, satisfying
$i=1,\ldots ,r$
, satisfying
Proof There is no loss of generality in assuming that A has the diagonal form
![]() $A=D \oplus D$
and
$A=D \oplus D$
and
![]() $S=I_{2n}$
. With this assumption, Proposition 3.2 gives the following representation of
$S=I_{2n}$
. With this assumption, Proposition 3.2 gives the following representation of
![]() $\tilde {S}$
in terms of a symplectic direct sum:
$\tilde {S}$
in terms of a symplectic direct sum:
 $$ \begin{align} \tilde{S} = \oplus^{\operatorname{s}}_i \begin{pmatrix} \tilde{S}_{\alpha_i \alpha_i} & \tilde{S}_{\alpha_i \beta_i} \\ -\tilde{S}_{\alpha_i \beta_i} & \tilde{S}_{\alpha_i \alpha_i} \end{pmatrix}+\mathcal{O}(\|H\|). \end{align} $$
$$ \begin{align} \tilde{S} = \oplus^{\operatorname{s}}_i \begin{pmatrix} \tilde{S}_{\alpha_i \alpha_i} & \tilde{S}_{\alpha_i \beta_i} \\ -\tilde{S}_{\alpha_i \beta_i} & \tilde{S}_{\alpha_i \alpha_i} \end{pmatrix}+\mathcal{O}(\|H\|). \end{align} $$
Our strategy is to apply the Gram–Schmidt orthonormalization process to the columns of
![]() $\tilde {S}_{\alpha _i \alpha _i}+\iota \tilde {S}_{\alpha _i \beta _i}$
to obtain a unitary matrix of the form
$\tilde {S}_{\alpha _i \alpha _i}+\iota \tilde {S}_{\alpha _i \beta _i}$
to obtain a unitary matrix of the form
![]() $U_{[i]}+\iota V_{[i]}$
, where
$U_{[i]}+\iota V_{[i]}$
, where
![]() $U_{[i]}$
and
$U_{[i]}$
and
![]() $V_{[i]}$
are real matrices, and then use the representation (2.1) to obtain orthosymplectic matrix
$V_{[i]}$
are real matrices, and then use the representation (2.1) to obtain orthosymplectic matrix
![]() $Q_{[i]}$
.
$Q_{[i]}$
.
Let
![]() $x_1,\ldots , x_{|\alpha _i|}$
and
$x_1,\ldots , x_{|\alpha _i|}$
and
![]() $y_1,\ldots , y_{|\alpha _i|}$
be the columns of
$y_1,\ldots , y_{|\alpha _i|}$
be the columns of
![]() $\tilde {S}_{\alpha _i \alpha _i}$
and
$\tilde {S}_{\alpha _i \alpha _i}$
and
![]() $\tilde {S}_{\alpha _i \beta _i}$
, respectively. Now, apply the Gram–Schmidt orthonormalization process to the complex vectors
$\tilde {S}_{\alpha _i \beta _i}$
, respectively. Now, apply the Gram–Schmidt orthonormalization process to the complex vectors
![]() $x_1+\iota y_1,\ldots , x_{|\alpha _i|}+\iota y_{|\alpha _i|}.$
Let
$x_1+\iota y_1,\ldots , x_{|\alpha _i|}+\iota y_{|\alpha _i|}.$
Let
![]() $z_1=x_1+\iota y_1$
. Choose
$z_1=x_1+\iota y_1$
. Choose
![]() $w_1=z_1/\|z_1\|\equiv u_1+\iota v_1$
. By (3.5) and (3.4), we have
$w_1=z_1/\|z_1\|\equiv u_1+\iota v_1$
. By (3.5) and (3.4), we have
 $$ \begin{align*} \|z_1\|^2 &=\|x_1\|^2+\|y_1\|^2 \\ &= \left\|\begin{pmatrix} x_1 \\ -y_1 \end{pmatrix}\right\|^2 =1+\mathcal{O}(\|H\|). \end{align*} $$
$$ \begin{align*} \|z_1\|^2 &=\|x_1\|^2+\|y_1\|^2 \\ &= \left\|\begin{pmatrix} x_1 \\ -y_1 \end{pmatrix}\right\|^2 =1+\mathcal{O}(\|H\|). \end{align*} $$
This implies
Let
![]() $z_{2}= x_2+\iota y_2 - \langle w_1, x_2+\iota y_2 \rangle w_1$
. Choose
$z_{2}= x_2+\iota y_2 - \langle w_1, x_2+\iota y_2 \rangle w_1$
. Choose
![]() $w_{2}=z_{2}/\|z_{2}\|\equiv u_2+\iota v_2$
so that
$w_{2}=z_{2}/\|z_{2}\|\equiv u_2+\iota v_2$
so that
![]() $\{w_1,w_2\}$
is an orthonormal set. By (3.5) and (3.4), we have
$\{w_1,w_2\}$
is an orthonormal set. By (3.5) and (3.4), we have
![]() $\langle x_1+\iota y_1, x_2+\iota y_2\rangle = \mathcal {O}(\|H\|)$
. This implies
$\langle x_1+\iota y_1, x_2+\iota y_2\rangle = \mathcal {O}(\|H\|)$
. This implies
 $$ \begin{align*} z_{2} &= x_2+\iota x_2 - \langle w_1, x_2+\iota y_2 \rangle w_1 \\ &= y_2+\iota y_2 - \langle x_1+\iota y_1, x_2+\iota y_2 \rangle w_1 + \mathcal{O}(\|H\|) \\ &= x_2+\iota y_2+\mathcal{O}(\|H\|). \end{align*} $$
$$ \begin{align*} z_{2} &= x_2+\iota x_2 - \langle w_1, x_2+\iota y_2 \rangle w_1 \\ &= y_2+\iota y_2 - \langle x_1+\iota y_1, x_2+\iota y_2 \rangle w_1 + \mathcal{O}(\|H\|) \\ &= x_2+\iota y_2+\mathcal{O}(\|H\|). \end{align*} $$
Again, by (3.5) and (3.4), we have
![]() $\|z_2\|=1+\mathcal {O}(\|H\|)$
, which implies
$\|z_2\|=1+\mathcal {O}(\|H\|)$
, which implies
![]() $w_{2}=x_2+\iota y_2+\mathcal {O}(\|H\|)$
.
$w_{2}=x_2+\iota y_2+\mathcal {O}(\|H\|)$
.
By continuing with the Gram–Schmidt process, we get orthonormal vectors
![]() $\{w_1, \ldots , w_{2|\alpha _i|}\}=\{u_1+\iota v_1,\ldots , u_{|\alpha _i|}+\iota v_{|\alpha _i|}\}$
such that for all
$\{w_1, \ldots , w_{2|\alpha _i|}\}=\{u_1+\iota v_1,\ldots , u_{|\alpha _i|}+\iota v_{|\alpha _i|}\}$
such that for all
![]() $j=1,\ldots , |\alpha _i|$
,
$j=1,\ldots , |\alpha _i|$
,
Let
,
so that
![]() $U_{[i]}+\iota V_{[i]}$
is a unitary matrix. By (2.1), it then follows that the following matrix:
$U_{[i]}+\iota V_{[i]}$
is a unitary matrix. By (2.1), it then follows that the following matrix:

is orthosymplectic. The relation (3.21) thus gives
 $$ \begin{align*} Q_{[i]}=\begin{pmatrix} \tilde{S}_{\alpha_i \alpha_i} & \tilde{S}_{\alpha_i \beta_i} \\ -\tilde{S}_{\alpha_i \beta_i} & \tilde{S}_{\alpha_i \alpha_i} \end{pmatrix}+\mathcal{O}(\|H\|). \end{align*} $$
$$ \begin{align*} Q_{[i]}=\begin{pmatrix} \tilde{S}_{\alpha_i \alpha_i} & \tilde{S}_{\alpha_i \beta_i} \\ -\tilde{S}_{\alpha_i \beta_i} & \tilde{S}_{\alpha_i \alpha_i} \end{pmatrix}+\mathcal{O}(\|H\|). \end{align*} $$
This combined with (3.20) gives
![]() $\tilde {S} = Q+\mathcal {O}(\|H\|),$
where
$\tilde {S} = Q+\mathcal {O}(\|H\|),$
where
![]() $Q=Q_{[1]} \oplus ^{\operatorname {s}} \cdots \oplus ^{\operatorname {s}} Q_{[r]}$
, which completes the proof.
$Q=Q_{[1]} \oplus ^{\operatorname {s}} \cdots \oplus ^{\operatorname {s}} Q_{[r]}$
, which completes the proof.
The matrix
![]() $SQ$
in Theorem 3.4 characterizes the set
$SQ$
in Theorem 3.4 characterizes the set
![]() $\operatorname {Sp}(2n; A)$
. We state this in the following proposition, proof of which follows directly from Corollary 5.3 of [Reference Jain and Mishra13]. It is also stated as Theorem 3.5 in [Reference Son, Absil, Gao and Stykel21].
$\operatorname {Sp}(2n; A)$
. We state this in the following proposition, proof of which follows directly from Corollary 5.3 of [Reference Jain and Mishra13]. It is also stated as Theorem 3.5 in [Reference Son, Absil, Gao and Stykel21].
Proposition 3.5 Let
![]() $S \in \operatorname {Sp}(2n; A)$
be fixed. Every symplectic matrix
$S \in \operatorname {Sp}(2n; A)$
be fixed. Every symplectic matrix
![]() $\hat {S} \in \operatorname {Sp}(2n; A)$
is precisely of the form
$\hat {S} \in \operatorname {Sp}(2n; A)$
is precisely of the form
where
![]() $Q=Q_{[1]} \oplus ^{\operatorname {s}} \cdots \oplus ^{\operatorname {s}} Q_{[r]}$
such that
$Q=Q_{[1]} \oplus ^{\operatorname {s}} \cdots \oplus ^{\operatorname {s}} Q_{[r]}$
such that
![]() $Q_{[i]}\in \operatorname {OrSp}(2|\alpha _i|)$
for all
$Q_{[i]}\in \operatorname {OrSp}(2|\alpha _i|)$
for all
![]() $i=1,\ldots , r$
.
$i=1,\ldots , r$
.
In [Reference Idel, Gaona and Wolf11], it is shown that if A has no repeated symplectic eigenvalues, then for any fixed
![]() $H \in \operatorname {Sm}(2n)$
, one can choose
$H \in \operatorname {Sm}(2n)$
, one can choose
![]() $S \in \operatorname {Sp}(2n; A)$
and
$S \in \operatorname {Sp}(2n; A)$
and
![]() $S(\varepsilon ) \in \operatorname {Sp}(2n; A+\varepsilon H)$
for small
$S(\varepsilon ) \in \operatorname {Sp}(2n; A+\varepsilon H)$
for small
![]() $\varepsilon>0$
such that
$\varepsilon>0$
such that
![]() $\|S(\varepsilon )-S\|=\mathcal {O}(\sqrt {\varepsilon })$
. We generalize their result to the more general case of A having repeated symplectic eigenvalues. Moreover, we consider the most general perturbation of A and strengthen the aforementioned result.
$\|S(\varepsilon )-S\|=\mathcal {O}(\sqrt {\varepsilon })$
. We generalize their result to the more general case of A having repeated symplectic eigenvalues. Moreover, we consider the most general perturbation of A and strengthen the aforementioned result.
Theorem 3.6 Let
![]() $A \in \operatorname {Pd}(2n)$
and
$A \in \operatorname {Pd}(2n)$
and
![]() $H\in \operatorname {Sm}(2n)$
such that
$H\in \operatorname {Sm}(2n)$
such that
![]() $A + H \in \operatorname {Pd}(2n).$
Given any
$A + H \in \operatorname {Pd}(2n).$
Given any
![]() $\tilde {S}\in \operatorname {Sp}(2n; A+H)$
, there exists
$\tilde {S}\in \operatorname {Sp}(2n; A+H)$
, there exists
![]() $S \in \operatorname {Sp}(2n; A)$
such that
$S \in \operatorname {Sp}(2n; A)$
such that
Proof Let
![]() $M \in \operatorname {Sp}(2n; A)$
. By Theorem 3.4, we have
$M \in \operatorname {Sp}(2n; A)$
. By Theorem 3.4, we have
where
![]() $Q=Q_{[1]} \oplus ^{\operatorname {s}} \cdots \oplus ^{\operatorname {s}} Q_{[r]}$
such that
$Q=Q_{[1]} \oplus ^{\operatorname {s}} \cdots \oplus ^{\operatorname {s}} Q_{[r]}$
such that
![]() $Q_{[i]}\in \operatorname {OrSp}(2|\alpha _i|)$
for all
$Q_{[i]}\in \operatorname {OrSp}(2|\alpha _i|)$
for all
![]() $i=1,\ldots , r$
. Set
$i=1,\ldots , r$
. Set
![]() so that
so that
![]() $\|\tilde {S}-S\|=\mathcal {O}(\|H\|)$
. We also have
$\|\tilde {S}-S\|=\mathcal {O}(\|H\|)$
. We also have
![]() $S \in \operatorname {Sp}(2n; A)$
which follows from Proposition 3.5.
$S \in \operatorname {Sp}(2n; A)$
which follows from Proposition 3.5.
We know from Theorem 3.4 that the distance of the symplectic block
![]() $\left (S^{-1}\tilde {S}\right )_{\gamma _i \gamma _i}$
from
$\left (S^{-1}\tilde {S}\right )_{\gamma _i \gamma _i}$
from
![]() $\operatorname {OrSp}(2|\alpha _i|)$
is
$\operatorname {OrSp}(2|\alpha _i|)$
is
![]() $\mathcal {O}(\|H\|)$
for all
$\mathcal {O}(\|H\|)$
for all
![]() $i=1,\ldots , r$
. Since
$i=1,\ldots , r$
. Since
![]() $ \operatorname {Sp}(2|\alpha _i|) \supset \operatorname {OrSp}(2|\alpha _i|)$
, the distance of
$ \operatorname {Sp}(2|\alpha _i|) \supset \operatorname {OrSp}(2|\alpha _i|)$
, the distance of
![]() $\left (S^{-1}\tilde {S}\right )_{\gamma _i \gamma _i}$
from
$\left (S^{-1}\tilde {S}\right )_{\gamma _i \gamma _i}$
from
![]() $\operatorname {Sp}(2|\alpha _i|)$
is expected to be even smaller. The following result shows that this distance is
$\operatorname {Sp}(2|\alpha _i|)$
is expected to be even smaller. The following result shows that this distance is
![]() $\mathcal {O}(\|H\|^2)$
.
$\mathcal {O}(\|H\|^2)$
.
Let
![]() $W=[u,v]$
be a
$W=[u,v]$
be a
![]() $2n \times 2$
matrix such that
$2n \times 2$
matrix such that
![]() $\operatorname {Range} (W)$
is non-isotropic, i.e.,
$\operatorname {Range} (W)$
is non-isotropic, i.e.,
![]() $u^TJ_{2n}v \neq 0.$
Let
$u^TJ_{2n}v \neq 0.$
Let
 $R=\begin {pmatrix}1 & 0 \\ 0 & u^TJ_{2n}v \end {pmatrix}$
and
$R=\begin {pmatrix}1 & 0 \\ 0 & u^TJ_{2n}v \end {pmatrix}$
and
![]() $S=WR^{-1}.$
We then have
$S=WR^{-1}.$
We then have
![]() $S \in \operatorname {Sp}(2n, 2)$
. The decomposition
$S \in \operatorname {Sp}(2n, 2)$
. The decomposition
![]() $W=SR$
is called the elementary SR decomposition (ESR). See [Reference Salam18] for various versions of ESR and their applications in symplectic analogs of the Gram–Schmidt method.
$W=SR$
is called the elementary SR decomposition (ESR). See [Reference Salam18] for various versions of ESR and their applications in symplectic analogs of the Gram–Schmidt method.
Proposition 3.7 Let
![]() $A \in \operatorname {Pd}(2n)$
and
$A \in \operatorname {Pd}(2n)$
and
![]() $H\in \operatorname {Sm}(2n)$
such that
$H\in \operatorname {Sm}(2n)$
such that
![]() $A + H \in \operatorname {Pd}(2n).$
Let
$A + H \in \operatorname {Pd}(2n).$
Let
![]() $S\in \operatorname {Sp}(2n; A)$
and
$S\in \operatorname {Sp}(2n; A)$
and
![]() $\tilde {S} \in \operatorname {Sp}(2n; A+H)$
. For each
$\tilde {S} \in \operatorname {Sp}(2n; A+H)$
. For each
![]() $i=1,\ldots ,r$
, there exists
$i=1,\ldots ,r$
, there exists
![]() $N_{[i]} \in \operatorname {Sp}(2|\alpha _i|)$
such that
$N_{[i]} \in \operatorname {Sp}(2|\alpha _i|)$
such that
Proof Without loss of generality, we can assume that A has the diagonal form
![]() ${A=D \oplus D}$
and
${A=D \oplus D}$
and
![]() $S=I_{2n}$
. Let
$S=I_{2n}$
. Let
![]() $u_1,\ldots ,u_{|\alpha _i|}, v_1, \ldots , v_{|\alpha _i|}$
be the columns of
$u_1,\ldots ,u_{|\alpha _i|}, v_1, \ldots , v_{|\alpha _i|}$
be the columns of
![]() $\tilde {S}_{\gamma _i \gamma _i}$
. Set
$\tilde {S}_{\gamma _i \gamma _i}$
. Set
![]() for
for
![]() $j=1,\ldots ,|\alpha _i|$
. We will apply mathematical induction on j to construct
$j=1,\ldots ,|\alpha _i|$
. We will apply mathematical induction on j to construct
![]() $N_{[i]}$
. We note that
$N_{[i]}$
. We note that
![]() $\tilde {S}_{\gamma _i \gamma _i}$
can be expressed as
$\tilde {S}_{\gamma _i \gamma _i}$
can be expressed as
Choose
![]() $W_{[1]}=M_{[1]}.$
We know from (3.5) that
$W_{[1]}=M_{[1]}.$
We know from (3.5) that
![]() $\operatorname {Range}(W_{[1]})$
is non-isotropic for small
$\operatorname {Range}(W_{[1]})$
is non-isotropic for small
![]() $\|H\|$
. Apply ESR to
$\|H\|$
. Apply ESR to
![]() $W_{[1]}$
to get
$W_{[1]}$
to get
![]() $W_{[1]} = S_{[1]}R_{[1]}$
, where
$W_{[1]} = S_{[1]}R_{[1]}$
, where
 $$ \begin{align} R_{[1]}&=\begin{pmatrix} 1 & 0 \\ 0 & u_1^TJ_{2|\alpha_i|}v_1\end{pmatrix}, \end{align} $$
$$ \begin{align} R_{[1]}&=\begin{pmatrix} 1 & 0 \\ 0 & u_1^TJ_{2|\alpha_i|}v_1\end{pmatrix}, \end{align} $$
and
![]() $S_{[1]}=W_{[1]} R_{[1]}^{-1} \in \operatorname {Sp}(2|\alpha _i|,2)$
. By (3.5), we have
$S_{[1]}=W_{[1]} R_{[1]}^{-1} \in \operatorname {Sp}(2|\alpha _i|,2)$
. By (3.5), we have
![]() $u_1^TJ_{2|\alpha _i|}v_1=1+\mathcal {O}(\|H\|^2)$
. Substituting this in (3.23) gives
$u_1^TJ_{2|\alpha _i|}v_1=1+\mathcal {O}(\|H\|^2)$
. Substituting this in (3.23) gives
Substituting the value of
![]() $R_{[1]}$
from (3.24) in
$R_{[1]}$
from (3.24) in
![]() $W_{[1]} = S_{[1]}R_{[1]}$
gives
$W_{[1]} = S_{[1]}R_{[1]}$
gives
Our induction hypothesis is that, for
![]() $1\leq j < |\alpha _i|$
, there exist
$1\leq j < |\alpha _i|$
, there exist
![]() $2|\alpha _i|\times 2$
real matrices
$2|\alpha _i|\times 2$
real matrices
![]() $S_{[1]},\ldots , S_{[j]}$
satisfying
$S_{[1]},\ldots , S_{[j]}$
satisfying
![]() $S_{[1]} \diamond \cdots \diamond S_{[j]} \in \operatorname {Sp}(2|\alpha _i|, 2j)$
and
$S_{[1]} \diamond \cdots \diamond S_{[j]} \in \operatorname {Sp}(2|\alpha _i|, 2j)$
and
We choose
which implies
![]() $\operatorname {Range}(W_{[j+1]})$
is non-isotropic for small
$\operatorname {Range}(W_{[j+1]})$
is non-isotropic for small
![]() $\mathcal {O}(\|H\|)$
. Apply ESR to
$\mathcal {O}(\|H\|)$
. Apply ESR to
![]() $W_{[j+1]}=[w_{j+1}, z_{j+1}]$
to get
$W_{[j+1]}=[w_{j+1}, z_{j+1}]$
to get
![]() $W_{[j+1]} = S_{[j+1]}R_{[j+1]}$
. Here,
$W_{[j+1]} = S_{[j+1]}R_{[j+1]}$
. Here,
![]() $S_{[j+1]} \in \operatorname {Sp}(2|\alpha _i|,2)$
and
$S_{[j+1]} \in \operatorname {Sp}(2|\alpha _i|,2)$
and
 $$ \begin{align} R_{[j+1]} &=\begin{pmatrix} 1 & 0 \\ 0 & w_{j+1}^TJ_{2|\alpha_i|}z_{j+1}\end{pmatrix}. \end{align} $$
$$ \begin{align} R_{[j+1]} &=\begin{pmatrix} 1 & 0 \\ 0 & w_{j+1}^TJ_{2|\alpha_i|}z_{j+1}\end{pmatrix}. \end{align} $$
From (3.5) and (3.27), we get
![]() $w_{j+1}^TJ_{2|\alpha _i|}z_{j+1}=1+ \mathcal {O}(\|H\|^2)$
. Using this relation in (3.28) implies
$w_{j+1}^TJ_{2|\alpha _i|}z_{j+1}=1+ \mathcal {O}(\|H\|^2)$
. Using this relation in (3.28) implies
![]() $R_{[j+1]}=I_2 + \mathcal {O}(\|H\|^2)$
. Substituting this in
$R_{[j+1]}=I_2 + \mathcal {O}(\|H\|^2)$
. Substituting this in
![]() $W_{[j+1]} = S_{[j+1]}R_{[j+1]}$
gives
$W_{[j+1]} = S_{[j+1]}R_{[j+1]}$
gives
Combining (3.27) and (3.29) then gives
We thus have
To complete the induction, we just need to show that
![]() $S_{[1]} \diamond \cdots \diamond S_{[j+1]} \in \operatorname {Sp}(2|\alpha _i|, 2(j+1))$
. We have
$S_{[1]} \diamond \cdots \diamond S_{[j+1]} \in \operatorname {Sp}(2|\alpha _i|, 2(j+1))$
. We have
By the necessary and sufficient condition for
![]() $(S_{[1]} \diamond \cdots \diamond S_{[j]}) \diamond S_{[j+1]} \in \operatorname {Sp}(2|\alpha _i|, 2(j+1))$
, as discussed in Section 2.3, it is equivalent to show that
$(S_{[1]} \diamond \cdots \diamond S_{[j]}) \diamond S_{[j+1]} \in \operatorname {Sp}(2|\alpha _i|, 2(j+1))$
, as discussed in Section 2.3, it is equivalent to show that
![]() $(S_{[1]} \diamond \cdots \diamond S_{[j]} )^T J_{2|\alpha _i|}S_{[j+1]}$
is the zero matrix. Now, using the relation
$(S_{[1]} \diamond \cdots \diamond S_{[j]} )^T J_{2|\alpha _i|}S_{[j+1]}$
is the zero matrix. Now, using the relation
![]() $W_{[j+1]} = S_{[j+1]}R_{[j+1]}$
, we get
$W_{[j+1]} = S_{[j+1]}R_{[j+1]}$
, we get
Substitute in (3.30), the value of
![]() $W_{[j+1]}$
from (3.26) to get
$W_{[j+1]}$
from (3.26) to get
 $$ \begin{align*} &\left(S_{[1]} \diamond \cdots \diamond S_{[j]} \right)^T J_{2|\alpha_i|}S_{[j+1]} =\left(S_{[1]} \diamond \cdots \diamond S_{[j]} \right)^T J_{2|\alpha_i|} \\ &\quad\left[M_{[j+1]}-\left(S_{[1]} \diamond \cdots \diamond S_{[j]} \right)J^T_{2j} \left(S_{[1]} \diamond \cdots \diamond S_{[j]} \right)^TJ_{2|\alpha_i|}M_{[j+1]}\right]R_{[j+1]}^{-1}. \end{align*} $$
$$ \begin{align*} &\left(S_{[1]} \diamond \cdots \diamond S_{[j]} \right)^T J_{2|\alpha_i|}S_{[j+1]} =\left(S_{[1]} \diamond \cdots \diamond S_{[j]} \right)^T J_{2|\alpha_i|} \\ &\quad\left[M_{[j+1]}-\left(S_{[1]} \diamond \cdots \diamond S_{[j]} \right)J^T_{2j} \left(S_{[1]} \diamond \cdots \diamond S_{[j]} \right)^TJ_{2|\alpha_i|}M_{[j+1]}\right]R_{[j+1]}^{-1}. \end{align*} $$
Apply the induction hypothesis
![]() $S_{[1]} \diamond \cdots \diamond S_{[j]} \in \operatorname {Sp}(2|\alpha _i|, 2j)$
and simplify as follows:
$S_{[1]} \diamond \cdots \diamond S_{[j]} \in \operatorname {Sp}(2|\alpha _i|, 2j)$
and simplify as follows:
 $$ \begin{align} &\left(S_{[1]} \diamond \cdots \diamond S_{[j]} \right)^T J_{2|\alpha_i|}S_{[j+1]} \nonumber \\ &=\left[\left(S_{[1]} \diamond \cdots \diamond S_{[j]} \right)^T J_{2|\alpha_i|} M_{[j+1]}-J_{2j} J^T_{2j} \left(S_{[1]} \diamond \cdots \diamond S_{[j]} \right)^TJ_{2|\alpha_i|}M_{[j+1]} \right]R_{[j+1]}^{-1} \nonumber \\ &=\left[\left(S_{[1]} \diamond \cdots \diamond S_{[j]} \right)^T J_{2|\alpha_i|} M_{[j+1]}- \left(S_{[1]} \diamond \cdots \diamond S_{[j]} \right)^TJ_{2|\alpha_i|}M_{[j+1]} \right]R_{[j+1]}^{-1} \nonumber \\ &= 0_{2j, 2}. \end{align} $$
$$ \begin{align} &\left(S_{[1]} \diamond \cdots \diamond S_{[j]} \right)^T J_{2|\alpha_i|}S_{[j+1]} \nonumber \\ &=\left[\left(S_{[1]} \diamond \cdots \diamond S_{[j]} \right)^T J_{2|\alpha_i|} M_{[j+1]}-J_{2j} J^T_{2j} \left(S_{[1]} \diamond \cdots \diamond S_{[j]} \right)^TJ_{2|\alpha_i|}M_{[j+1]} \right]R_{[j+1]}^{-1} \nonumber \\ &=\left[\left(S_{[1]} \diamond \cdots \diamond S_{[j]} \right)^T J_{2|\alpha_i|} M_{[j+1]}- \left(S_{[1]} \diamond \cdots \diamond S_{[j]} \right)^TJ_{2|\alpha_i|}M_{[j+1]} \right]R_{[j+1]}^{-1} \nonumber \\ &= 0_{2j, 2}. \end{align} $$
We have thus shown that
![]() $S_{[1]} \diamond \cdots \diamond S_{[j+1]} \in \operatorname {Sp}(2|\alpha _i|, 2(j+1))$
. By induction, we then get the desired matrix
$S_{[1]} \diamond \cdots \diamond S_{[j+1]} \in \operatorname {Sp}(2|\alpha _i|, 2(j+1))$
. By induction, we then get the desired matrix
![]() $N_{[i]}=S_{[1]} \diamond \cdots \diamond S_{[|\alpha _i|]} \in \operatorname {Sp}(2|\alpha _i|)$
, which satisfies
$N_{[i]}=S_{[1]} \diamond \cdots \diamond S_{[|\alpha _i|]} \in \operatorname {Sp}(2|\alpha _i|)$
, which satisfies
4 Conclusion
One of the main findings of our work is that, given any
![]() $S\in \operatorname {Sp}(2n; A)$
and
$S\in \operatorname {Sp}(2n; A)$
and
![]() $\tilde {S} \in \operatorname {Sp}(2n; A+H)$
, there exists an orthosymplectic matrix Q such that
$\tilde {S} \in \operatorname {Sp}(2n; A+H)$
, there exists an orthosymplectic matrix Q such that
![]() $\tilde {S}=SQ+\mathcal {O}(\|H\|)$
. Moreover, the orthosymplectic matrix Q has structure
$\tilde {S}=SQ+\mathcal {O}(\|H\|)$
. Moreover, the orthosymplectic matrix Q has structure
![]() $Q=Q_{[1]} \oplus ^s \cdots \oplus ^s Q_{[r]}$
, where
$Q=Q_{[1]} \oplus ^s \cdots \oplus ^s Q_{[r]}$
, where
![]() $Q_{[j]}$
is a
$Q_{[j]}$
is a
![]() $2|\alpha _j| \times 2 |\alpha _j|$
orthosymplectic matrix. Here, r is the number of distinct symplectic eigenvalues
$2|\alpha _j| \times 2 |\alpha _j|$
orthosymplectic matrix. Here, r is the number of distinct symplectic eigenvalues
![]() $\mu _1,\ldots , \mu _r$
of A and
$\mu _1,\ldots , \mu _r$
of A and
![]() $\alpha _j$
is the set of indices of the symplectic eigenvalues of A equal to
$\alpha _j$
is the set of indices of the symplectic eigenvalues of A equal to
![]() $\mu _j$
. We also proved that
$\mu _j$
. We also proved that
![]() $S\in \operatorname {Sp}(2n; A)$
and
$S\in \operatorname {Sp}(2n; A)$
and
![]() $\tilde {S} \in \operatorname {Sp}(2n; A+H)$
can be chosen so that
$\tilde {S} \in \operatorname {Sp}(2n; A+H)$
can be chosen so that
![]() $\|\tilde {S}-S\|=\mathcal {O}(\|H\|)$
.
$\|\tilde {S}-S\|=\mathcal {O}(\|H\|)$
.
Acknowledgments
The authors are grateful to Prof. Tanvi Jain for the insightful discussions that took place in the initial stage of the work. The authors thank Prof. Mark M. Wilde for pointing out some mistakes during the preparation of the manuscript and Dr. Tiju Cherian John for some critical comments. The authors are thankful to the anonymous referee for their thoughtful comments and suggestions that improved the readability of the paper.