Published online by Cambridge University Press: 20 April 2023
A classical theorem of Balcar, Pelant, and Simon says that there is a base matrix of height 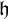 ${\mathfrak h}$, where
${\mathfrak h}$, where 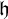 ${\mathfrak h}$ is the distributivity number of
${\mathfrak h}$ is the distributivity number of 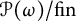 ${\cal P} (\omega ) / {\mathrm {fin}}$. We show that if the continuum
${\cal P} (\omega ) / {\mathrm {fin}}$. We show that if the continuum 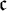 ${\mathfrak c}$ is regular, then there is a base matrix of height
${\mathfrak c}$ is regular, then there is a base matrix of height 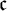 ${\mathfrak c}$, and that there are base matrices of any regular uncountable height
${\mathfrak c}$, and that there are base matrices of any regular uncountable height 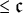 $\leq {\mathfrak c}$ in the Cohen and random models. This answers questions of Fischer, Koelbing, and Wohofsky.
$\leq {\mathfrak c}$ in the Cohen and random models. This answers questions of Fischer, Koelbing, and Wohofsky.
This work was partially supported by Grant-in-Aid for Scientific Research (C) 18K03398 from the Japan Society for the Promotion of Science.