Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-25T18:18:27.421Z Has data issue: false hasContentIssue false
  • English
  • Français

Band-Limited Wavelets with Subexponential Decay

Published online by Cambridge University Press:  20 November 2018

Jacek Dziubański  and
Eugenio Hernández
Jacek Dziubański
Affiliation:
Instytut Matematyczny Uniwersytet Wroclawski 50-384 Wroclaw Poland, e-mail: [email protected]
Eugenio Hernández
Affiliation:
Departamento Matemáticas Universidad Autónoma de Madrid 28049 Madrid Spain, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

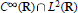It is well known that the compactly supported wavelets cannot belong to the class ${{C}^{\infty }}\,(\text{R})\,\cap \,{{L}^{2}}\,(R)$. This is also true for wavelets with exponential decay. We show that one can construct wavelets in the class 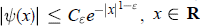${{C}^{\infty }}\,(\text{R})\,\cap \,{{L}^{2}}\,(R)$ that are “almost” of exponential decay and, moreover, they are band-limited. We do this by showing that we can adapt the construction of the Lemarié-Meyer wavelets 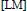$[\text{LM }\!\!]\!\!\text{ }$ that is found in 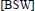$[\text{BSW}]$ so that we obtain band-limited, 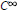${{C}^{\infty }}$-wavelets on 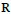$R$ that have subexponential decay, that is, for every 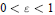$0<\varepsilon <1$, there exits 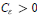${{C}_{\in }}\,>\,0$ such that 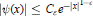$|\psi (x)|\le {{C}_{\varepsilon }}{{e}^{-|x{{|}^{1-\varepsilon }}}}$, 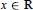$x\in \text{R}$. Moreover, all of its derivatives have also subexponential decay. The proof is constructive and uses the Gevrey classes of functions.

Keywords

42C15WaveletGevrey classessubexponential decay
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 41 , Issue 4 , 01 December 1998 , pp. 398 - 403
Copyright
Copyright © Canadian Mathematical Society 1998

References

[AWW] Auscher, P., Weiss, G. and Wickerhauser, M. V., Local sine and cosine basis of Coifman and Meyer and the construction of smooth wavelets. In:Wavelets: A tutorial in theory and applications, (ed. C.K. Chui), Academic Press, (1992), 237–256.Google Scholar
[BSW] Bonami, A., Soria, F. and Weiss, G., Band-limited wavelets. J. Geom. Anal. (6) 3 (1993), 544–578.Google Scholar
[Da] Daubechies, I., Orthonormal bases of compactly supported wavelets. Comm. Pure Appl. Math. 41 (1988), 909–996.Google Scholar
[Ho1] Hörmander, L., The analysis of linear partial differential operators I. Springer-Verlag, 1983.Google Scholar
[Ho2] Hörmander, L., The analysis of linear partial differential operators II. Springer-Verlag, 1983.Google Scholar
[HW] Hernández, E. and Weiss, G., A first course on wavelets. CRC Press, 1996.Google Scholar
[Le] Lemarié-Rieusset, P. G., Ondelettes à localisation exponentielles, J.Math. Pures Appl. 67 (1988), 227–236.Google Scholar
[LM] Lemarié, P. G. and Meyer, Y., Ondelettes et bases hilbertiennes, Rev. Mat. Iberoamericana 2 (1986), 1–18.Google Scholar