Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Gröchenig, Karlheinz
and
Haas, Andrew
1996.
Backward continued fractions, Hecke groups and invariant measures for transformations of the interval.
Ergodic Theory and Dynamical Systems,
Vol. 16,
Issue. 6,
p.
1241.
Burton, Robert
Kraaikamp, Cornelis
and
Schmidt, Thomas
1999.
Natural extensions for the Rosen fractions.
Transactions of the American Mathematical Society,
Vol. 352,
Issue. 3,
p.
1277.
Arnoux, Pierre
and
Hubert, Pascal
2000.
Fractions continues sur les surfaces de Veech.
Journal d'Analyse Mathématique,
Vol. 81,
Issue. 1,
p.
35.
Ramharter, G.
2005.
Maximal continuants and the Fine–Wilf theorem.
Journal of Combinatorial Theory, Series A,
Vol. 111,
Issue. 1,
p.
59.
Arnoux, Pierre
and
Schmidt, Thomas A.
2014.
Commensurable continued fractions.
Discrete and Continuous Dynamical Systems,
Vol. 34,
Issue. 11,
p.
4389.


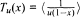 on [0,1). We first show that the dynamics of the shift map on a specific class of shift invariant spaces of nonnegative integer sequences exactly models the maps
on [0,1). We first show that the dynamics of the shift map on a specific class of shift invariant spaces of nonnegative integer sequences exactly models the maps 