Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-26T06:34:42.079Z Has data issue: false hasContentIssue false
  • English
  • Français

Automorphisms of Metabelian Groups

Published online by Cambridge University Press:  20 November 2018

Athanassios I. Papistas
Athanassios I. Papistas*
Affiliation:
Department of Mathematics Aristotle University of Thessaloniki GR 540 06, Thessaloniki Greece, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We investigate the problem of determining when 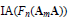$\text{IA}({{F}_{n}}({{\mathbf{A}}_{m}}\mathbf{A}))$ is finitely generated for all 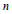$n$ and 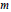$m$, with 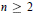$n\ge 2$ and 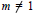$m\ne 1$. If 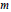$m$ is a nonsquare free integer then 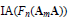$\text{IA}({{F}_{n}}({{\mathbf{A}}_{m}}\mathbf{A}))$ is not finitely generated for all 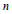$n$ and if 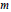$m$ square free integer then 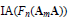$\text{IA}({{F}_{n}}({{\mathbf{A}}_{m}}\mathbf{A}))$ is finitely generated for all 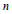$n$, with 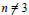$n\ne 3$, and 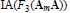$\text{IA}({{F}_{3}}({{\mathbf{A}}_{m}}\mathbf{A}))$ is not finitely generated. In case 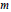$m$ is square free, Bachmuth and Mochizuki claimed in ([7], Problem 4) that 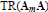$\text{TR}({{\mathbf{A}}_{m}}\mathbf{A})$ is 1 or 4. We correct their assertion by proving that 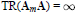$\text{TR}({{\mathbf{A}}_{m}}\mathbf{A})=\infty$.

Keywords

20F28
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 41 , Issue 1 , 01 March 1998 , pp. 98 - 104
Copyright
Copyright © Canadian Mathematical Society 1998

References

1. Bachmuth, S., Automorphisms of free metabelian groups. Trans. Amer.Math. Soc. 118 (1965), 93–104.Google Scholar
2. Bachmuth, S., Automorphisms of a class of metabelian groups. Trans. Amer.Math. Soc. 127 (1967), 284–293.Google Scholar
3. Bachmuth, S., Baumslag, G., Dyer, J. and Mochizuki, H. Y., Automorphisms of 2-generator metabelian groups. J. London Math. Soc. 36 (1987), 393–406.Google Scholar
4. Bachmuth, S. and Mochizuki, H. Y., Automorphisms of a class of metabelian groups II. Trans. Amer. Math. Soc. 127 (1967), 294–301.Google Scholar
5. Bachmuth, S. and Mochizuki, H. Y., IA-automorphisms of free metabelian group of rank 3. J. Algebra 55 (1979), 106–115.Google Scholar
6. Bachmuth, S. and Mochizuki, H. Y., Aut(F)! Aut(FÛF00) is surjective for free groups F of rank n ½ 4. Trans. Amer. Math. Soc. 292 (1985), 81–101.Google Scholar
7. Bachmuth, S. and Mochizuki, H. Y., The tame range of automorphism groups and GLn .Group Theory Proc.Singapore Group Theory Conf., 1987, 241–251, de Gruyter, New York, 1989.Google Scholar
8. Bachmuth, S. and Mochizuki, H. Y., Infinite generation of automorphism groups. Proceedings of Groups Korea 1988, Pusan, 1988, 25–28, Lecture Notes in Math. 1398, Springer, Berlin, New York, 1989.Google Scholar
9. Bryant, R. M. and Groves, J. R. J., Automorphisms of free metabelian groups of infinite rank. Comm. Algebra (11) 18 (1990), 3619–3631.Google Scholar
10. Cohen, D. E., Subgroups of HNN-groups. J. Austral. Math. Soc. 17 (1974), 394–405.Google Scholar
11. Karrass, A. and Solitar, D., The subgroups of a free product of two groups with an amalgamated subgroup. Trans. Amer. Math. Soc. 150 (1970), 227–255.Google Scholar
12. Karrass, A. and Solitar, D. Subgroups of HNN-groups and groups with one defining relation. Canad. J. Math. 23(1971), 627–543.Google Scholar
13. Krasnikov, A. F., Nilpotent subgroups of relatively free groups. Algebra i Logika 17(1978), 389–401.Google Scholar