Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-24T10:40:14.875Z Has data issue: false hasContentIssue false
  • English
  • Français

Atomic Decomposition and Boundedness of Operators on Weighted Hardy Spaces

Published online by Cambridge University Press:  20 November 2018

Yongsheng Han ,
Ming-Yi Lee  and
Chin-Cheng Lin
Yongsheng Han
Affiliation:
Department of Mathematics, Auburn University, Auburn, AL 36849-5310, U.S.A.e-mail: [email protected]
Ming-Yi Lee
Affiliation:
Department of Mathematics, National Central University, Chung-Li, Taiwan 320, Republic of Chinae-mail: [email protected]; [email protected]
Chin-Cheng Lin
Affiliation:
Department of Mathematics, National Central University, Chung-Li, Taiwan 320, Republic of Chinae-mail: [email protected]; [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

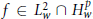In this article, we establish a new atomic decomposition for $f\,\in \,L_{w}^{2}\,\bigcap \,H_{w}^{p}$, where the decomposition converges in 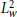$L_{w}^{2}$-norm rather than in the distribution sense. As applications of this decomposition, assuming that 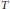$T$ is a linear operator bounded on 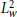$L_{w}^{2}$ and 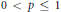$0\,<\,p\,\le \,1$, we obtain (i) if 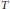$T$ is uniformly bounded in 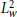$L_{w}^{p}$-norm for all 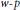$w-p$-atoms, then 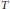$T$ can be extended to be bounded from 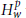$H_{w}^{p}$ to 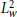$L_{w}^{2}$; (ii) if 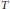$T$ is uniformly bounded in 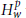$H_{w}^{p}$-norm for all 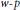$w-p$-atoms, then 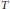$T$ can be extended to be bounded on 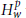$H_{w}^{p}$; (iii) if 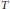$T$ is bounded on 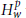$H_{w}^{p}$, then 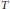$T$ can be extended to be bounded from 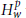$H_{w}^{p}$ to 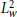$L_{w}^{2}$.

Keywords

42B2542B30Ap weightsatomic decompositionCalderón reproducing formulaweighted Hardy spaces
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 55 , Issue 2 , 01 June 2012 , pp. 303 - 314
Copyright
Copyright © Canadian Mathematical Society 2012

References

[1] Coifman, R. R., A real variable characterization of Hp . Studia Math. 51(1974), 269–274.Google Scholar
[2] Fefferman, C. and Stein, E. M., Hp spaces of several variables. Acta Math. 129(1972), 137–193. http://dx.doi.org/10.1007/BF02392215 Google Scholar
[3] Frazier, M., Jawerth, B., and Weiss, G., Littlewood-Paley Theory and the Study of Function Spaces. CBMS Regional Conference Series in Mathematics 79. American Mathematical Society, Providence, RI, 1991.Google Scholar
[4] Garcia-Cuerva, J., Weighted Hp spaces. Dissertations Math. 162(1979), 1–63.Google Scholar
[5] Garcia-Cuerva, J. and Martell, J. M., Wavelet characterization of weighted spaces. J. Geom. Anal. 11(2001), no. 2, 241–264.Google Scholar
[6] García-Cuerva, J. and Rubio de Francia, J. L., Weighted Norm Inequalities and Related Topics. North-Holland Mathematics Studies 116. North-Holland, Amsterdam, 1985.Google Scholar
[7] Gundy, R. F. and Wheeden, R. L., Weighted integral inequalities for the nontangential maximal function, Lusin area integral, and Walsh-Paley series. Studia Math. 49(1973/1974), 107–124.Google Scholar
[8] Han, Y. S. and Sawyer, E. T., Littlewood-Paley theory on spaces of homogeneous type and classical function spaces. Mem. Amer. Math. Soc. 110(1994), no. 530.Google Scholar
[9] Latter, R. H., A characterization of Hp (ℝ n in terms of atoms. Studia Math. 62(1978), no. 1, 93–101.Google Scholar
[10] Lee, M.-Y. and Lin, C.-C., The molecular characterization of weighted Hardy spaces. J. Funct. Anal. 188(2002), no. 2, 442–460. http://dx.doi.org/10.1006/jfan.2001.3839 Google Scholar
[11] Meyer, Y., Ondelettes et opérateurs. II. Hermann, Paris, 1990.Google Scholar
[12] Stein, E. M., Singular Integrals and Differentiability Properties of Functions. Princeton Mathematical Series 30. Princeton University Press, Princeton, New Jersey, 1970.Google Scholar
[13] Stein, E. M. and Weiss, G., On the theory of harmonic functions of several variables. I. The theory of Hp-spaces. Acta Math. 103(1960), 25–62. http://dx.doi.org/10.1007/BF02546524 Google Scholar
[14] Strömberg, J.-O. and Torchinsky, A., Weighted Hardy Spaces. Lecture Notes in Math. 1381. Springer-Verlag, Berlin, 1989.Google Scholar