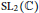Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Tange, Ryoto
Tran, Anh T
and
Ueki, Jun
2022.
Non-acyclic SL2-representations of Twist Knots, -3-Dehn Surgeries, and L-functions.
International Mathematics Research Notices,
Vol. 2022,
Issue. 15,
p.
11690.