Hostname: page-component-66644f4456-tnr8b Total loading time: 0 Render date: 2025-02-12T21:06:01.029Z Has data issue: true hasContentIssue false
  • English
  • Français

Asymptotic Improvements of Lower Bounds for the Least Common Multiples of Arithmetic Progressions

Published online by Cambridge University Press:  20 November 2018

Daniel M. Kane  and
Scott Duke Kominers
Daniel M. Kane
Affiliation:
Department of Mathematics, Stanford University, Stanford, CA 94305, USA e-mail: [email protected]@gmail.com
Scott Duke Kominers
Affiliation:
Department of Economics, Program for Evolutionary Dynamics and Center for Research on Computation and Society, Harvard University and Harvard Business School, Cambridge, MA 02138-3758, USA e-mail: [email protected]@gmail.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For relatively prime positive integers 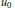${{u}_{0}}$ and $r$, we consider the least common multiple 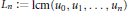${{L}_{n}}\,:=\,\text{lcm}\left( {{u}_{0}},\,{{u}_{1}},\,.\,.\,.\,,\,{{u}_{n}} \right)$ of the finite arithmetic progression 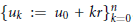$\left\{ {{u}_{k}}\,:=\,{{u}_{0}}\,+\,kr \right\}_{k=0}^{n}$. We derive new lower bounds on 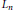${{L}_{n}}$ that improve upon those obtained previously when either 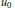${{u}_{0}}$ or $n$ is large. When $r$ is prime, our best bound is sharp up to a factor of 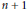$n\,+\,1$ for 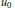${{u}_{0}}$ properly chosen, and is also nearly sharp as 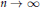$n\,\to \,\infty$.

Keywords

11A05least common multiplearithmetic progression
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 57 , Issue 3 , 01 September 2014 , pp. 551 - 561
Copyright
Copyright © Canadian Mathematical Society 2014

References

[BKS02] Bateman, P., Kalb, J., and Stenger, A., A limit involving least common multiples: 10797. Amer. Math. Monthly 109 (2002), no. 4, 393–394. http://dx.doi.org/10.2307/2695513 Google Scholar
[Far05] Farhi, B., Minorations non triviales du plus petit commun multiple de certaines suites finies d’entiers. C. R. Math. Acad. Sci. Paris 341 (2005), no. 8, 469–474. http://dx.doi.org/10.1016/j.crma.2005.09.019 Google Scholar
[Far07] Farhi, B., Nontrivial lower bounds for the least common multiple of some finite sequences of integers. J. Number Theory 125 (2007), no. 2, 393–411. http://dx.doi.org/10.1016/j.jnt.2006.10.017 Google Scholar
[FK09] Farhi, B. and Kane, D., New results on the least common multiple of consecutive integers. Proc. Amer. Math. Soc. 137 (2009), no. 6, 1933–1939. http://dx.doi.org/10.1090/S0002-9939-08-09730-X Google Scholar
[Han72] Hanson, D., On the product of the primes. Canad. Math. Bull. 15 (1972), 33–37. http://dx.doi.org/10.4153/CMB-1972-007-7 Google Scholar
[HF06] Hong, S. and Feng, W., Lower bounds for the least common multiple of finite arithmetic progressions. C. R. Acad. Sci. Paris 343 (2006), no. 11–12, 695–698. http://dx.doi.org/10.1016/j.crma.2006.11.002 Google Scholar
[HK10] Hong, S. and Kominers, S. D., Further improvements of lower bounds for the least common multiples of arithmetic progressions. Proc. Amer. Math. Soc. 138 (2010), no. 3, 809–813. http://dx.doi.org/10.1090/S0002-9939-09-10083-7 Google Scholar
[HQ11] Hong, S. and Qian, G., The least common multiple of consecutive arithmetic progression terms. Proc. Edinb. Math. Soc. (2) 54 (2011), no. 2, 431–441. http://dx.doi.org/10.1017/S0013091509000431 Google Scholar
[HY08] Hong, S. and Yang, Y., Improvements of lower bounds for the least common multiple of finite arithmetic progressions. Proc. Amer. Math. Soc. 136 (2008), no. 12, 4111–4114. http://dx.doi.org/10.1090/S0002-9939-08-09565-8 Google Scholar
[IK04] Iwaniec, H. and Kowalski, E., Analytic number theory. American Mathematical Society Colloquium Publications, 53, American Mathematical Society, Providence, RI, 2004.Google Scholar
[Nai82] Nair, M., On Chebyshev-type inequalities for primes. Amer. Math. Monthly 89 (1982), no. 2, 126–129. http://dx.doi.org/10.2307/2320934 Google Scholar
[WTH13] Wu, R., Tan, Q., and Hong, S., New lower bounds for the least common multiples of arithmetic progressions. Chin. Ann. Math. Ser. B 34 (2013), no. 6, 861–864. http://dx.doi.org/10.1007/s11401-013-0805-9 Google Scholar