Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-26T06:11:40.489Z Has data issue: false hasContentIssue false
  • English
  • Français

Artinian Local Cohomology Modules

Published online by Cambridge University Press:  20 November 2018

Keivan Borna Lorestani ,
Parviz Sahandi  and
Siamak Yassemi
Keivan Borna Lorestani
Affiliation:
Department of Mathematics, University of Tehran, Tehran, Iran e-mail: [email protected]
Parviz Sahandi
Affiliation:
Center of Excellence in Biomathematics, School of Mathematics, Statistics and Computer Science, University of Tehran, Tehran, Iran andSchool of Mathematics, Institute for Studies in Theoretical Physics and Mathematics, Tehran, Iran e-mail: [email protected]@ipm.ir
Siamak Yassemi
Affiliation:
Center of Excellence in Biomathematics, School of Mathematics, Statistics and Computer Science, University of Tehran, Tehran, Iran andSchool of Mathematics, Institute for Studies in Theoretical Physics and Mathematics, Tehran, Iran e-mail: [email protected]@ipm.ir
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 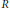$R$ be a commutative Noetherian ring, $\mathfrak{a}$ an ideal of 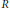$R$ and 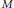$M$ a finitely generated 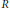$R$-module. Let 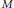$t$ be a non-negative integer. It is known that if the local cohomology module 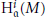$\text{H}_{\mathfrak{a}}^{i}\,\left( M \right)$ is finitely generated for all 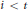$i\,<\,t$, then 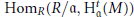$\text{Ho}{{\text{m}}_{R}}\,\left( R/\mathfrak{a},\,\text{H}_{\mathfrak{a}}^{t}\,\left( M \right) \right)$ is finitely generated. In this paper it is shown that if 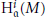$\text{H}_{\mathfrak{a}}^{i}\,\left( M \right)$ is Artinian for all 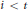$i\,<\,t$, then 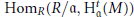$\text{Ho}{{\text{m}}_{R}}\,\left( R/\mathfrak{a},\,\text{H}_{\mathfrak{a}}^{t}\,\left( M \right) \right)$ need not be Artinian, but it has a finitely generated submodule 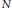$N$ such that 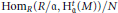$\text{Ho}{{\text{m}}_{R}}\left( R/\mathfrak{a},\text{H}_{\mathfrak{a}}^{t}\left( M \right) \right)/N$ is Artinian.

Keywords

13D4513E1013C05local cohomology moduleArtinian modulereflexive module
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 50 , Issue 4 , 01 December 2007 , pp. 598 - 602
Copyright
Copyright © Canadian Mathematical Society 2007

References

[AKS] Asadollahi, J., Khashyarmanesh, K., Salarian, Sh., A generalization of the cofiniteness problem in local cohomology modules. J. Aust. Math. Soc. 75(2003), no. 3, 313–324.Google Scholar
[B] Belshoff, R., Some change of ring theorems for Matlis reflexive modules. Comm. Algebra 22(1994), no. 9, 3545–3552.Google Scholar
[BER] Belshoff, R., Enochs, E. E., and Rozas, J. R. García, Generalized Matlis duality. Proc. Amer. Math. Soc. 128(2000), no. 5, 1307–1312.Google Scholar
[BL] Brodmann, M. P. and Faghani, A. L., A finiteness result for associated primes of local cohomology modules. Proc. Amer. Math. Soc. 128(2000), no. 10, 2851–2853.Google Scholar
[BS] Brodmann, M. P. and Sharp, R. Y., Local Cohomology: An Algebraic Introduction with Geometric Applications. Cambridge Studies in Advanced Mathematics 60, Cambridge University Press, Cambridge, 1998.Google Scholar
[G] Grothendieck, A., Cohomologie locale des faisceaux cohérents et théorèmes de Lefschetz locaux et globaux (SGA 2). Advanced Studies in Pure Mathematics, vol. 2, North-Holland, Amsterdam 1968.Google Scholar
[H] Hartshorne, R., Affine duality and cofiniteness. Invent. Math. 9(1969/1970) 145–164.Google Scholar
[KS] Khashyarmanesh, K. and Salarian, Sh., On the associated primes of local cohomology modules. Comm. Algebra 27(1999), no. 12, 6191–6198.Google Scholar
[M] Melkersson, L., Some application of a criterion for Artinianness of a module. J. Pure and Appl. Algebra 101(1995), no. 3, 291–303.Google Scholar
[R] Rudlof, P., On minimax and related modules. Canad. J. Math. 44 1992), no. 1, 154–166.Google Scholar
[X] Xue, W., Generalized Matlis duality and linear compactness. Comm. Algebra 30(2002), no. 4, 2075–2084.Google Scholar
[Z] Zöschinger, H., Minimax-moduln. J. Algebra 102(1986), no. 1, 1–32.Google Scholar