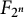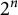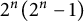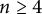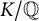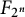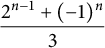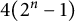1 Introduction
The following theorem concerning coincidence of Hecke L-functions is proved in [Reference Katayama and Kida6].
Theorem 1.1 Let p be a prime number. If
![]() $K/\mathbb {Q}$
is a Galois extension whose Galois group G is isoclinic to the Heisenberg group of order
$K/\mathbb {Q}$
is a Galois extension whose Galois group G is isoclinic to the Heisenberg group of order
![]() $p^3$
, then there are
$p^3$
, then there are
![]() $p+1$
abelian normal subgroups
$p+1$
abelian normal subgroups
![]() $H_i \ (i=1,\ldots ,p+1 )$
of index p in G and characters
$H_i \ (i=1,\ldots ,p+1 )$
of index p in G and characters
![]() $\chi _i $
of
$\chi _i $
of
![]() $H_i$
such that
$H_i$
such that
![]() $p+1$
Hecke L-functions
$p+1$
Hecke L-functions
![]() $L (\chi _i, s)$
coincide up to a finite number of Euler factors.
$L (\chi _i, s)$
coincide up to a finite number of Euler factors.
A natural question arises from this theorem.
Question Are there arbitrarily large number of number fields whose Dedekind zeta functions coincide?
Two number fields K and
![]() $K'$
are called arithmetically equivalent (over
$K'$
are called arithmetically equivalent (over
![]() $\mathbb {Q}$
) if the Dedekind zeta functions of
$\mathbb {Q}$
) if the Dedekind zeta functions of
![]() $K $
and
$K $
and
![]() $K'$
coincide. Conjugate number fields obviously have the same Dedekind zeta functions; thus, we are interested in nonconjugate arithmetically equivalent fields. Many examples of such fields are known until now (see [Reference Klingen8, Examples in III.1.b]), but examples of three or more arithmetically equivalent fields seem not to be known. The aim of this paper is to give such examples systematically.
$K'$
coincide. Conjugate number fields obviously have the same Dedekind zeta functions; thus, we are interested in nonconjugate arithmetically equivalent fields. Many examples of such fields are known until now (see [Reference Klingen8, Examples in III.1.b]), but examples of three or more arithmetically equivalent fields seem not to be known. The aim of this paper is to give such examples systematically.
To state our result more precisely, we introduce some notation. Let
![]() $\mathbb {F}_{2^n}$
be a finite field of
$\mathbb {F}_{2^n}$
be a finite field of
![]() $2^n $
elements. We consider the Frobenius group
$2^n $
elements. We consider the Frobenius group
![]() $F_{2^n}$
defined by
$F_{2^n}$
defined by
where
![]() $\mathbb {F}_{2^n}^{\times }$
acts faithfully on
$\mathbb {F}_{2^n}^{\times }$
acts faithfully on
![]() $\mathbb {F}_{2^n} $
. The group
$\mathbb {F}_{2^n} $
. The group
![]() $F_{2^n}$
can be described also as an affine linear group over
$F_{2^n}$
can be described also as an affine linear group over
![]() $\mathbb {F}_{2^n}$
:
$\mathbb {F}_{2^n}$
:
 $$ \begin{align} F_{2^n} \cong \mathrm{AGL}_1 (\mathbb{F}_{2^n}) = \left\{ \left. \begin{bmatrix} a & b \\ 0 & 1 \end{bmatrix} \in \mathrm{GL}_2 (\mathbb{F}_{2^n}) \ \right| \ a \in \mathbb{F}_{2^n}^{\times} , \ b \in \mathbb{F}_{2^n} \right\}. \end{align} $$
$$ \begin{align} F_{2^n} \cong \mathrm{AGL}_1 (\mathbb{F}_{2^n}) = \left\{ \left. \begin{bmatrix} a & b \\ 0 & 1 \end{bmatrix} \in \mathrm{GL}_2 (\mathbb{F}_{2^n}) \ \right| \ a \in \mathbb{F}_{2^n}^{\times} , \ b \in \mathbb{F}_{2^n} \right\}. \end{align} $$
The Frobenius kernel N is isomorphic to
 $$\begin{align*}\left\{ \left. \begin{bmatrix} 1 & b \\ 0 & 1 \end{bmatrix} \in \mathrm{AGL}_1 (\mathbb{F}_{2^n}) \right| \ \ b \in \mathbb{F}_{2^n} \right\} \cong \mathbb{F}_2^{n}, \end{align*}$$
$$\begin{align*}\left\{ \left. \begin{bmatrix} 1 & b \\ 0 & 1 \end{bmatrix} \in \mathrm{AGL}_1 (\mathbb{F}_{2^n}) \right| \ \ b \in \mathbb{F}_{2^n} \right\} \cong \mathbb{F}_2^{n}, \end{align*}$$
and a Frobenius complement H is isomorphic to
 $$\begin{align*}\left\{ \ \left. \begin{bmatrix} a & 0 \\ 0 & 1 \end{bmatrix} \in \mathrm{AGL}_1 (\mathbb{F}_{2^n}) \ \right| \ \ a \in \mathbb{F}_{2^n}^{\times} \right\} \cong \mathbb{F}_{2^{n}}^{\times}. \end{align*}$$
$$\begin{align*}\left\{ \ \left. \begin{bmatrix} a & 0 \\ 0 & 1 \end{bmatrix} \in \mathrm{AGL}_1 (\mathbb{F}_{2^n}) \ \right| \ \ a \in \mathbb{F}_{2^n}^{\times} \right\} \cong \mathbb{F}_{2^{n}}^{\times}. \end{align*}$$
Let
![]() $K/\mathbb {Q}$
be a Galois extension with Galois group isomorphic to the Frobenius group
$K/\mathbb {Q}$
be a Galois extension with Galois group isomorphic to the Frobenius group
![]() $F_{2^n}$
. Such an extension
$F_{2^n}$
. Such an extension
![]() $K/\mathbb {Q}$
is called an
$K/\mathbb {Q}$
is called an
![]() $F_{2^n}$
-extension. The fixed field L of K by the Frobenius kernel N is a cyclic extension of degree
$F_{2^n}$
-extension. The fixed field L of K by the Frobenius kernel N is a cyclic extension of degree
![]() $2^n-1$
over
$2^n-1$
over
![]() $\mathbb {Q}$
and
$\mathbb {Q}$
and
![]() $\operatorname {\mathrm {Gal}} (K/L)$
is isomorphic to an elementary abelian 2-group of rank n.
$\operatorname {\mathrm {Gal}} (K/L)$
is isomorphic to an elementary abelian 2-group of rank n.
Our main theorem is the following.
Theorem 1.2 Let n be an integer greater than
![]() $3$
. Among intermediate fields M of an
$3$
. Among intermediate fields M of an
![]() $F_{2^n}$
-extension
$F_{2^n}$
-extension
![]() $K/\mathbb {Q}$
with
$K/\mathbb {Q}$
with
![]() $[M:L]=4$
, there are
$[M:L]=4$
, there are
![]() $\dfrac {2^{n-1}+(-1)^n}{3}$
fields which are not conjugate but arithmetically equivalent.
$\dfrac {2^{n-1}+(-1)^n}{3}$
fields which are not conjugate but arithmetically equivalent.
As a matter of fact, there are several nonconjugate arithmetically equivalent fields of degree
![]() $2^s (s=2,\ldots , n-2)$
over L inside K. We concentrate the smallest degree fields for simplicity both in the proof and in the construction. Our proof and construction are explicit and specific throughout, and this enables us to find families of a large number of nonconjugate arithmetically equivalent fields explicitly.
$2^s (s=2,\ldots , n-2)$
over L inside K. We concentrate the smallest degree fields for simplicity both in the proof and in the construction. Our proof and construction are explicit and specific throughout, and this enables us to find families of a large number of nonconjugate arithmetically equivalent fields explicitly.
The outline of the paper is as follows. In the next section, we prove Theorem 1.2 in a refined form (Theorem 2.4) by using mainly the representation theory of finite groups. In Section 3, we discuss how to construct
![]() $F_{2^n}$
-extensions. We show that if a cyclic extension L is constructed, then we can construct infinitely many
$F_{2^n}$
-extensions. We show that if a cyclic extension L is constructed, then we can construct infinitely many
![]() $F_{2^n}$
-extensions containing L by using Kummer theory (Theorem 3.3). Our discussion here is explicit and constructive for the argument in the following section. In Section 4, we explain how to find nonconjugate arithmetically equivalent fields in an
$F_{2^n}$
-extensions containing L by using Kummer theory (Theorem 3.3). Our discussion here is explicit and constructive for the argument in the following section. In Section 4, we explain how to find nonconjugate arithmetically equivalent fields in an
![]() $F_{2^n}$
-extension and give an explicit description of these fields (Proposition 4.1).
$F_{2^n}$
-extension and give an explicit description of these fields (Proposition 4.1).
Throughout this paper, we use the following notation. We fix an integer n greater than
![]() $3$
. The Frobenius group of degree
$3$
. The Frobenius group of degree
![]() $2^n$
and of order
$2^n$
and of order
![]() $2^n (2^n-1)$
is denoted by
$2^n (2^n-1)$
is denoted by
![]() $F_{2^n} = H \ltimes N$
with H and N defined in the above.
$F_{2^n} = H \ltimes N$
with H and N defined in the above.
2 The proof of the main theorem
In this section, we shall prove Theorem 1.2. Let
![]() $K/\mathbb {Q} $
be an
$K/\mathbb {Q} $
be an
![]() $F_{2^n}$
-extension. We fix an isomorphism between
$F_{2^n}$
-extension. We fix an isomorphism between
![]() $\operatorname {\mathrm {Gal}} (K/\mathbb {Q})$
and
$\operatorname {\mathrm {Gal}} (K/\mathbb {Q})$
and
![]() $F_{2^n} = H \ltimes N$
and identify them by the isomorphism. Let L be the fixed field
$F_{2^n} = H \ltimes N$
and identify them by the isomorphism. Let L be the fixed field
![]() $K^N$
. The extension
$K^N$
. The extension
![]() $L/\mathbb {Q} $
is a cyclic extension of degree
$L/\mathbb {Q} $
is a cyclic extension of degree
![]() $2^n-1$
. The Galois group of
$2^n-1$
. The Galois group of
![]() $K/L$
is isomorphic to an elementary abelian
$K/L$
is isomorphic to an elementary abelian
![]() $2$
-group N of rank n, since the additive group of the field
$2$
-group N of rank n, since the additive group of the field
![]() $\mathbb {F}_{2^n}$
is isomorphic to
$\mathbb {F}_{2^n}$
is isomorphic to
![]() $\mathbb {F}_2^n$
.
$\mathbb {F}_2^n$
.
In this section, we use the following notation from the representation theory of finite groups. For a finite group G, we denote by
![]() $\mathrm {Irr} (G)$
the set of the irreducible character of G and by
$\mathrm {Irr} (G)$
the set of the irreducible character of G and by
![]() $1_G$
the principal character of G. For a character
$1_G$
the principal character of G. For a character
![]() $\psi $
of a subgroup E of G, we denote the induced character from
$\psi $
of a subgroup E of G, we denote the induced character from
![]() $\psi $
to G by
$\psi $
to G by
![]() $\psi ^G$
and for a character
$\psi ^G$
and for a character
![]() $\chi $
of G, the restriction of
$\chi $
of G, the restriction of
![]() $\chi $
to E by
$\chi $
to E by
![]() $\chi _E$
.
$\chi _E$
.
We begin by showing that all intermediate fields M of
![]() $K/\mathbb {Q} $
with
$K/\mathbb {Q} $
with
![]() $[M:L]=4$
are arithmetically equivalent. By [Reference Klingen8, Theorem III.1.3], it suffices to show the following proposition.
$[M:L]=4$
are arithmetically equivalent. By [Reference Klingen8, Theorem III.1.3], it suffices to show the following proposition.
Proposition 2.1 Let n be an integer greater than
![]() $3$
. Let
$3$
. Let
![]() $G=F_{2^n} = H \ltimes N$
. If E is a subgroup of N of order
$G=F_{2^n} = H \ltimes N$
. If E is a subgroup of N of order
![]() $2^{n-2}$
, then the induced character
$2^{n-2}$
, then the induced character
![]() $1_E^G$
is independent of the choice of E and hence the characters
$1_E^G$
is independent of the choice of E and hence the characters
![]() $1_E^G$
are equal for all E.
$1_E^G$
are equal for all E.
Note that the group E in Proposition 2.1 is core-free, that is,
![]() $ \mathrm {Core}_G (E) = \bigcap _{g \in G} (g E g^{-1}) = 1$
, and thus the character
$ \mathrm {Core}_G (E) = \bigcap _{g \in G} (g E g^{-1}) = 1$
, and thus the character
![]() $1_E^G$
is a faithful permutation character. This also implies that the Galois closure of
$1_E^G$
is a faithful permutation character. This also implies that the Galois closure of
![]() $K^E$
coincides with K.
$K^E$
coincides with K.
To prove the proposition, we use the following fact on the representation of Frobenius groups, which is a special case of [Reference Huppert4, Satz V.16.13].
Lemma 2.2 The irreducible characters of
![]() $F_{2^n} = H \ltimes N$
consist of linear characters
$F_{2^n} = H \ltimes N$
consist of linear characters
![]() $\mu _i \ (i \in \{ 0,\ldots , 2^n-2 \})$
which are extensions of
$\mu _i \ (i \in \{ 0,\ldots , 2^n-2 \})$
which are extensions of
![]() $\eta _i \in \mathrm {Irr} (H)$
with
$\eta _i \in \mathrm {Irr} (H)$
with
![]() $\ker \mu _i \supset N$
and a character
$\ker \mu _i \supset N$
and a character
![]() $\psi $
of degree
$\psi $
of degree
![]() $2^n-1$
induced from a nontrivial character
$2^n-1$
induced from a nontrivial character
![]() $\varphi $
of N such that
$\varphi $
of N such that
![]() $\psi _N = \sum _{h \in H} \varphi ^h$
.
$\psi _N = \sum _{h \in H} \varphi ^h$
.
Proof of Proposition 2.1
We compute the inner product of
![]() $1_E^G$
and
$1_E^G$
and
![]() $\chi \in \mathrm {Irr} (G)$
by Frobenius reciprocity:
$\chi \in \mathrm {Irr} (G)$
by Frobenius reciprocity:
Let
![]() $\mu _i$
and
$\mu _i$
and
![]() $ \psi $
be the characters as in Lemma 2.2. Since
$ \psi $
be the characters as in Lemma 2.2. Since
![]() $E \subset N$
, we have
$E \subset N$
, we have
 $$\begin{align*}(1_E^G, \mu_i )_G= \frac{2^{n-2}}{|E|}=1. \end{align*}$$
$$\begin{align*}(1_E^G, \mu_i )_G= \frac{2^{n-2}}{|E|}=1. \end{align*}$$
If
![]() $\chi = \psi $
, then we can write
$\chi = \psi $
, then we can write
![]() $\psi = \varphi ^G$
with
$\psi = \varphi ^G$
with
![]() $\varphi (\neq 1_N) \in \mathrm {Irr} (N)$
. It is clear that
$\varphi (\neq 1_N) \in \mathrm {Irr} (N)$
. It is clear that
![]() $\psi (1) = [G : N ] =2^n-1$
. For a nontrivial element
$\psi (1) = [G : N ] =2^n-1$
. For a nontrivial element
![]() $x \in E \subset N$
, we have
$x \in E \subset N$
, we have
Here, the second equality holds since the action of H on N is transitive and faithful, and therefore the set
![]() $\{ hxh^{-1} \mid h \in H \}$
coincides with
$\{ hxh^{-1} \mid h \in H \}$
coincides with
![]() $N-\{1\}$
. Moreover, the third equality follows from the fact that
$N-\{1\}$
. Moreover, the third equality follows from the fact that
![]() $\varphi $
is nontrivial. We conclude
$\varphi $
is nontrivial. We conclude
 $$ \begin{align*} (1_E^G, \psi )_G &= \frac{1}{2^{n-2}} \left(\psi (1) + \sum_{x (\neq 1) \in E} \psi (x) \right)\\[6pt] & = \frac{1}{2^{n-2}} (2^n-1 + (-1)(2^{n-2}-1)) = 3. \end{align*} $$
$$ \begin{align*} (1_E^G, \psi )_G &= \frac{1}{2^{n-2}} \left(\psi (1) + \sum_{x (\neq 1) \in E} \psi (x) \right)\\[6pt] & = \frac{1}{2^{n-2}} (2^n-1 + (-1)(2^{n-2}-1)) = 3. \end{align*} $$
Consequently, we obtain the decomposition of
![]() $1_E^G$
:
$1_E^G$
:
 $$\begin{align*}1_E^G = 3 \psi + \sum_{i=0}^{2^n-2} \mu_i , \end{align*}$$
$$\begin{align*}1_E^G = 3 \psi + \sum_{i=0}^{2^n-2} \mu_i , \end{align*}$$
which is independent of the choice of E. This completes the proof of Proposition 2.1.▪
We have an immediate corollary by [Reference Klingen8, Theorem III.1.3].
Corollary 2.3 All quartic extensions over L contained in K are arithmetically equivalent.
We now enumerate such quartic fields up to conjugacy. We shall prove a more precise version of Theorem 1.2.
Theorem 2.4 For each quadratic extension F over L in K, there are
![]() $2^{n-1}-1$
quartic extensions M over L with
$2^{n-1}-1$
quartic extensions M over L with
![]() $F \subset M \subset K$
.
$F \subset M \subset K$
.
-
(i) If n is odd, then they are divided into
 $\dfrac {2^{n-1}-1}{3}$
conjugacy classes over
$\dfrac {2^{n-1}-1}{3}$
conjugacy classes over
 $\mathbb {Q}$
containing three fields in each class. By choosing one field from each conjugacy class,
$\mathbb {Q}$
containing three fields in each class. By choosing one field from each conjugacy class,
 $\dfrac {2^{n-1}-1}{3}$
fields are nonconjugate and arithmetically equivalent.
$\dfrac {2^{n-1}-1}{3}$
fields are nonconjugate and arithmetically equivalent. -
(ii) If n is even, then they are divided into
 $\dfrac {2^{n-1}-2}{3}$
conjugacy classes over
$\dfrac {2^{n-1}-2}{3}$
conjugacy classes over
 $\mathbb {Q}$
containing three fields in each class, and the other conjugacy class consists of the remaining one field. By choosing one field from each conjugacy class,
$\mathbb {Q}$
containing three fields in each class, and the other conjugacy class consists of the remaining one field. By choosing one field from each conjugacy class,
 $\dfrac {2^{n-1}+1}{3}$
fields are nonconjugate and arithmetically equivalent.
$\dfrac {2^{n-1}+1}{3}$
fields are nonconjugate and arithmetically equivalent.
We have already showed their arithmetic equivalence in Corollary 2.3. By Galois theory, we only have to prove the following group-theoretic version of Theorem 2.4.
Theorem 2.5 Let
![]() $\mathscr {E}$
be the set of the subgroups of order
$\mathscr {E}$
be the set of the subgroups of order
![]() $2^{n-2}$
of N. The group G acts on
$2^{n-2}$
of N. The group G acts on
![]() $\mathscr {E}$
through
$\mathscr {E}$
through
![]() $\mathbb {F}_{2^n}^{\times }$
. Let D be a subgroup of N of order
$\mathbb {F}_{2^n}^{\times }$
. Let D be a subgroup of N of order
![]() $2^{n-1}$
. We have
$2^{n-1}$
. We have
![]() $|\mathscr {E} \cap D| =2^{n-1}-1$
with obvious abuse of notation.
$|\mathscr {E} \cap D| =2^{n-1}-1$
with obvious abuse of notation.
-
(i) If n is odd, then the set
 $\mathscr {E}$
is divided into
$\mathscr {E}$
is divided into
 $\dfrac {2^{n-1}-1}{3}$
conjugacy classes under G and the classes C satisfy
$\dfrac {2^{n-1}-1}{3}$
conjugacy classes under G and the classes C satisfy
 $|C \cap D|=3$
.
$|C \cap D|=3$
. -
(ii) If n is even, then the set
 $\mathscr {E}$
is divided into
$\mathscr {E}$
is divided into
 $\dfrac {2^{n-1}+1}{3}$
conjugacy classes under G, the
$\dfrac {2^{n-1}+1}{3}$
conjugacy classes under G, the
 $\dfrac {2^{n-1}-2}{3}$
conjugacy classes C satisfy
$\dfrac {2^{n-1}-2}{3}$
conjugacy classes C satisfy
 $|C \cap D|=3$
, and the rest of the classes
$|C \cap D|=3$
, and the rest of the classes
 $C'$
satisfies
$C'$
satisfies
 $|C' \cap D|=1$
.
$|C' \cap D|=1$
.
Proof It is well known that the number of t-dimensional subspaces in an s-dimensional vector space over
![]() $\mathbb {F}_2$
is given by the q-binomial coefficient with
$\mathbb {F}_2$
is given by the q-binomial coefficient with
![]() $q=2$
, which we denote by
$q=2$
, which we denote by
 $$\begin{align*}\begin{bmatrix} s \\ t \end{bmatrix} = \frac{(2^s-1) (2^{s-1}-1) \cdots (2^{s-t+1}-1)} {(2^t-1)(2^{t-1}-1)\cdots (2-1)}. \end{align*}$$
$$\begin{align*}\begin{bmatrix} s \\ t \end{bmatrix} = \frac{(2^s-1) (2^{s-1}-1) \cdots (2^{s-t+1}-1)} {(2^t-1)(2^{t-1}-1)\cdots (2-1)}. \end{align*}$$
Using this formula, we can compute
 $$ \begin{align*} |\mathscr{E}| & = \begin{bmatrix} n \\ n -2 \end{bmatrix} = \begin{bmatrix} n \\ 2 \end{bmatrix}= \frac{1}{3} (2^n-1)(2^{n-1}-1) \end{align*} $$
$$ \begin{align*} |\mathscr{E}| & = \begin{bmatrix} n \\ n -2 \end{bmatrix} = \begin{bmatrix} n \\ 2 \end{bmatrix}= \frac{1}{3} (2^n-1)(2^{n-1}-1) \end{align*} $$
and
 $$ \begin{align*} |\mathscr{E} \cap D| & = \begin{bmatrix} n-1 \\ n-2 \end{bmatrix} = \begin{bmatrix} n-1 \\ 1 \end{bmatrix} = 2^{n-1}-1. \end{align*} $$
$$ \begin{align*} |\mathscr{E} \cap D| & = \begin{bmatrix} n-1 \\ n-2 \end{bmatrix} = \begin{bmatrix} n-1 \\ 1 \end{bmatrix} = 2^{n-1}-1. \end{align*} $$
Now, we identify N with the additive group of
![]() $\mathbb {F}_{2^n}$
. If g is a generator of
$\mathbb {F}_{2^n}$
. If g is a generator of
![]() $\mathbb {F}_{2^n}^{\times }$
and
$\mathbb {F}_{2^n}^{\times }$
and
![]() ${E \in \mathscr {E}}$
, then we can write
${E \in \mathscr {E}}$
, then we can write
![]() $E=\{ 0, g^{i_1}, \ldots ,g^{i_{2^{n-2}-1}}\}$
with
$E=\{ 0, g^{i_1}, \ldots ,g^{i_{2^{n-2}-1}}\}$
with
![]() $\{ i_1, \ldots , i_{2^{n-2}-1}\} \subset \{ 1,2,\ldots , 2^n-1 \}$
. For notational convenience, we write it as
$\{ i_1, \ldots , i_{2^{n-2}-1}\} \subset \{ 1,2,\ldots , 2^n-1 \}$
. For notational convenience, we write it as
![]() $E= (i_1, \ldots , i_{2^{n-2}-1})$
. If we represent
$E= (i_1, \ldots , i_{2^{n-2}-1})$
. If we represent
![]() $\tau \in G$
by a product
$\tau \in G$
by a product
![]() $ g^{\ell } \nu \ (g^{\ell } \in H, \nu \in N)$
, then it is easy to see that the conjugate
$ g^{\ell } \nu \ (g^{\ell } \in H, \nu \in N)$
, then it is easy to see that the conjugate
![]() $E^{\tau } $
is given by
$E^{\tau } $
is given by
![]() $E^{\tau } = E^{g^{\ell }} =(i_1 + \ell , \ldots , i_{2^{n-2}-1}+\ell )$
. We compute the normalizer
$E^{\tau } = E^{g^{\ell }} =(i_1 + \ell , \ldots , i_{2^{n-2}-1}+\ell )$
. We compute the normalizer
![]() $N_G (E)$
. We have
$N_G (E)$
. We have
![]() $\tau = g^{\ell } \nu \in N_G (E)$
if and only if there exists a permutation
$\tau = g^{\ell } \nu \in N_G (E)$
if and only if there exists a permutation
![]() $\gamma \in S_{2^{n-2}-1}$
such that
$\gamma \in S_{2^{n-2}-1}$
such that
Summing up both the sides for j, we obtain
and this yields
![]() $(2^{n-2} -1 ) \ell \equiv 0 \pmod {2^n-1}$
. In this connection, we see
$(2^{n-2} -1 ) \ell \equiv 0 \pmod {2^n-1}$
. In this connection, we see
 $$\begin{align*}\gcd (2^{n-2}-1 , 2^n -1)= \gcd (2^n-1, 3) = \begin{cases} 1, & \text{ if } n \text{ is odd}, \\ 3, & \text{ if } n \text{ is even}. \end{cases} \end{align*}$$
$$\begin{align*}\gcd (2^{n-2}-1 , 2^n -1)= \gcd (2^n-1, 3) = \begin{cases} 1, & \text{ if } n \text{ is odd}, \\ 3, & \text{ if } n \text{ is even}. \end{cases} \end{align*}$$
Therefore, if n is odd, then we conclude that
![]() $\ell =0 $
and
$\ell =0 $
and
![]() $N_G (E) = N$
. Hence, the orbit length of every
$N_G (E) = N$
. Hence, the orbit length of every
![]() $E \in \mathscr {E}$
is
$E \in \mathscr {E}$
is
![]() $2^n-1$
, and the set
$2^n-1$
, and the set
![]() $\mathscr {E}$
is divided into
$\mathscr {E}$
is divided into
![]() $\dfrac {1}{3} (2^{n-1}-1)$
conjugacy classes.
$\dfrac {1}{3} (2^{n-1}-1)$
conjugacy classes.
If n is even, then we obtain
![]() $\ell =0 $
or
$\ell =0 $
or
![]() $\dfrac {2^n-1}{3}$
. In the latter case, the element
$\dfrac {2^n-1}{3}$
. In the latter case, the element
![]() $g^{\ell }$
in
$g^{\ell }$
in
![]() $N_G (E)$
is of order
$N_G (E)$
is of order
![]() $3$
. Accordingly, the orbit length of E is either
$3$
. Accordingly, the orbit length of E is either
![]() $2^n-1$
or
$2^n-1$
or
![]() $\dfrac {2^n-1}{3}$
. Let u (resp. v) be the number of orbits of length
$\dfrac {2^n-1}{3}$
. Let u (resp. v) be the number of orbits of length
![]() $2^n-1 \left ( \text {resp. } \dfrac {2^n-1}{3} \right )$
. It obviously yields
$2^n-1 \left ( \text {resp. } \dfrac {2^n-1}{3} \right )$
. It obviously yields
We compute the total number of orbits
![]() $u+v$
by using the lemma of Burnside–Frobenius [Reference Aigner1, Lemma 6.2]. For
$u+v$
by using the lemma of Burnside–Frobenius [Reference Aigner1, Lemma 6.2]. For
![]() $x \in G$
, if we define
$x \in G$
, if we define
then we have
As is seen in the above, we have
![]() $ \mathrm {Fix} (g^i \nu ) = \mathrm {Fix} (g^i) $
if we write
$ \mathrm {Fix} (g^i \nu ) = \mathrm {Fix} (g^i) $
if we write
![]() $x =g^i \nu $
with
$x =g^i \nu $
with
![]() $\nu \in N$
. Moreover, if the order of
$\nu \in N$
. Moreover, if the order of
![]() $g^i$
is neither
$g^i$
is neither
![]() $1$
nor
$1$
nor
![]() $3$
, then
$3$
, then
![]() $ \mathrm {Fix} (x) = \emptyset $
. Obviously, if the order of
$ \mathrm {Fix} (x) = \emptyset $
. Obviously, if the order of
![]() $g^i$
is equal to
$g^i$
is equal to
![]() $1$
, then we have
$1$
, then we have
![]() $i=0$
and
$i=0$
and
![]() $\mathrm {Fix} (1) = \mathscr {E}$
.
$\mathrm {Fix} (1) = \mathscr {E}$
.
We now suppose that the order of
![]() $g^i$
is
$g^i$
is
![]() $3$
, and thus
$3$
, and thus
![]() $i=(2^n-1)/3$
. Since the minimal polynomial of
$i=(2^n-1)/3$
. Since the minimal polynomial of
![]() $g^i$
over
$g^i$
over
![]() $\mathbb {F}_2$
is
$\mathbb {F}_2$
is
![]() $X^2+X+1$
of degree
$X^2+X+1$
of degree
![]() $2$
, the irreducible
$2$
, the irreducible
![]() $\langle g^i \rangle $
-module B is of dimension
$\langle g^i \rangle $
-module B is of dimension
![]() $2$
over
$2$
over
![]() $\mathbb {F}_2$
. It is easy to see that B is of the form
$\mathbb {F}_2$
. It is easy to see that B is of the form
![]() $\{ 0 , g^t , g^{t+i}, g^{t+2i}\}$
with some
$\{ 0 , g^t , g^{t+i}, g^{t+2i}\}$
with some
![]() $ 0 \le t \le 2^n-1$
. Since one of
$ 0 \le t \le 2^n-1$
. Since one of
![]() $t , {t+i}, {t+2i}$
modulo
$t , {t+i}, {t+2i}$
modulo
![]() $2^n-1$
lies in the first one-third interval, we may assume that
$2^n-1$
lies in the first one-third interval, we may assume that
![]() $ 0 \le t < (2^n-1)/3$
. Hence, there are
$ 0 \le t < (2^n-1)/3$
. Hence, there are
![]() $\dfrac {2^n-1}{3}$
distinct irreducible
$\dfrac {2^n-1}{3}$
distinct irreducible
![]() $\langle g^i \rangle $
-modules inside N. To compute
$\langle g^i \rangle $
-modules inside N. To compute
![]() $|\mathrm {Fix} (g^i)|$
, we have to enumerate
$|\mathrm {Fix} (g^i)|$
, we have to enumerate
![]() $(n-2)$
-dimensional
$(n-2)$
-dimensional
![]() $\langle g^i \rangle $
- modules inside N, but instead we only have to enumerate the complementary two-dimensional modules by Maschke’s theorem [Reference Isaacs5, Theorem 1.9]. Therefore, we conclude
$\langle g^i \rangle $
- modules inside N, but instead we only have to enumerate the complementary two-dimensional modules by Maschke’s theorem [Reference Isaacs5, Theorem 1.9]. Therefore, we conclude
![]() $|\mathrm {Fix} (g^i)| = \dfrac {2^n-1}{3}$
.
$|\mathrm {Fix} (g^i)| = \dfrac {2^n-1}{3}$
.
Therefore, it follows that
 $$ \begin{align} \qquad u+v = \frac{2^n}{2^n(2^n-1)} \sum_{i=0}^{2^n-2} |\mathrm{Fix} (g^i)| = \frac{1}{2^n-1} \left( |\mathscr{E}| + 2 \times \dfrac{2^n-1}{3} \right) = \frac{2^{n-1}+1}{3}. \end{align} $$
$$ \begin{align} \qquad u+v = \frac{2^n}{2^n(2^n-1)} \sum_{i=0}^{2^n-2} |\mathrm{Fix} (g^i)| = \frac{1}{2^n-1} \left( |\mathscr{E}| + 2 \times \dfrac{2^n-1}{3} \right) = \frac{2^{n-1}+1}{3}. \end{align} $$
Solving equations (2.1) and (2.2), we obtain
We conclude that there are
![]() $\dfrac {2}{3} (2^{n-2} -1)$
conjugacy classes of length
$\dfrac {2}{3} (2^{n-2} -1)$
conjugacy classes of length
![]() $2^n-1$
and one conjugacy class of length
$2^n-1$
and one conjugacy class of length
![]() $\dfrac {2^n-1}{3}$
.
$\dfrac {2^n-1}{3}$
.
Let
![]() $\mathscr {O}$
be an orbit in
$\mathscr {O}$
be an orbit in
![]() $\mathscr {E}$
. Since G acts on the set of D’s transitively by Singer’s theorem [Reference Hall3, Theorem 11.3.1], the number
$\mathscr {E}$
. Since G acts on the set of D’s transitively by Singer’s theorem [Reference Hall3, Theorem 11.3.1], the number
![]() $|\mathscr {O} \cap D| $
is independent of the choice of D.
$|\mathscr {O} \cap D| $
is independent of the choice of D.
We first consider the case where n is odd. Let
![]() $\mathscr {O}_i \ (i=1,\ldots ,(2^{n-1}-1)/3)$
be the conjugacy classes. Since
$\mathscr {O}_i \ (i=1,\ldots ,(2^{n-1}-1)/3)$
be the conjugacy classes. Since
 $$ \begin{align} \sum_{i=1}^{(2^{n-1}-1)/3} | \mathscr{O}_i \cap D | = | \mathscr{E} \cap D| \end{align} $$
$$ \begin{align} \sum_{i=1}^{(2^{n-1}-1)/3} | \mathscr{O}_i \cap D | = | \mathscr{E} \cap D| \end{align} $$
holds, it follows
Hence, we conclude that
![]() $| \mathscr {O}_i \cap D |=3$
, namely each D contains three conjugate fields.
$| \mathscr {O}_i \cap D |=3$
, namely each D contains three conjugate fields.
Next, we consider the case where n is even. Let
![]() $\mathscr {O}_i \ ( i=1,\ldots ,{2}(2^{n-2}-1)/3 )$
be the conjugacy classes of length
$\mathscr {O}_i \ ( i=1,\ldots ,{2}(2^{n-2}-1)/3 )$
be the conjugacy classes of length
![]() $2^n-1$
, and let
$2^n-1$
, and let
![]() $\mathscr {P}$
be the conjugacy class of length
$\mathscr {P}$
be the conjugacy class of length
![]() $(2^n-1)/3$
. If
$(2^n-1)/3$
. If
![]() $E \in \mathscr {P}$
, then it is invariant by an element of order
$E \in \mathscr {P}$
, then it is invariant by an element of order
![]() $3$
in
$3$
in
![]() $\mathbb {F}_{2^n}^{\times }$
. Therefore, such E is contained in three different D’s. Since there are
$\mathbb {F}_{2^n}^{\times }$
. Therefore, such E is contained in three different D’s. Since there are
![]() $2^n-1$
nonconjugate D’s, we conclude that
$2^n-1$
nonconjugate D’s, we conclude that
![]() $|\mathscr {P} \cap D|=1$
. This also yields an equation like (2.3):
$|\mathscr {P} \cap D|=1$
. This also yields an equation like (2.3):
 $$\begin{align*}\sum_{i=1}^{2(2^{n-2}-1)/3} | \mathscr{O}_i \cap D | = |\mathscr{E} \cap D | -1. \end{align*}$$
$$\begin{align*}\sum_{i=1}^{2(2^{n-2}-1)/3} | \mathscr{O}_i \cap D | = |\mathscr{E} \cap D | -1. \end{align*}$$
From this, it follows
![]() $|\mathscr {O}_i \cap D | =3$
for all i.
$|\mathscr {O}_i \cap D | =3$
for all i.
This completes the proof of Theorem 2.5, and thus Theorems 1.2 and 2.4 follow.▪
Remark 2.6 Theorem 1.2 holds even if the base field is not
![]() $\mathbb {Q}$
. However, in that case, we cannot define the arithmetic equivalence by the coincidence of the Dedekind zeta functions. See [Reference Klingen8, Theorem III.1.3].
$\mathbb {Q}$
. However, in that case, we cannot define the arithmetic equivalence by the coincidence of the Dedekind zeta functions. See [Reference Klingen8, Theorem III.1.3].
3 Construction of
 $F_{2^n}$
-extensions
$F_{2^n}$
-extensions
In this section, we construct
![]() $F_{2^n}$
-extensions for every n. The method is an extension of those used in [Reference Kida7, Reference Nakano and Sase9], where only metacyclic extensions are constructed.
$F_{2^n}$
-extensions for every n. The method is an extension of those used in [Reference Kida7, Reference Nakano and Sase9], where only metacyclic extensions are constructed.
The method fully works for a general base field k whose characteristic is not
![]() $2$
. Thus, we assume that
$2$
. Thus, we assume that
![]() $G=\operatorname {\mathrm {Gal}} (K/k) = F_{2^n} = H \ltimes N$
and
$G=\operatorname {\mathrm {Gal}} (K/k) = F_{2^n} = H \ltimes N$
and
![]() $L=K^N$
, and that a cyclic extension
$L=K^N$
, and that a cyclic extension
![]() $L/k$
has been constructed.
$L/k$
has been constructed.
In the case
![]() $k=\mathbb {Q}$
, if we take a prime number
$k=\mathbb {Q}$
, if we take a prime number
![]() $\ell $
satisfying
$\ell $
satisfying
![]() $\ell \equiv 1 \pmod {2^{n}-1}$
, there is a unique cyclic field L of degree
$\ell \equiv 1 \pmod {2^{n}-1}$
, there is a unique cyclic field L of degree
![]() $2^{n}-1$
inside the
$2^{n}-1$
inside the
![]() $\ell $
th cyclotomic field. Furthermore, there exist infinitely many such prime numbers
$\ell $
th cyclotomic field. Furthermore, there exist infinitely many such prime numbers
![]() $\ell $
for each n by Dirichlet’s theorem on arithmetic progression.
$\ell $
for each n by Dirichlet’s theorem on arithmetic progression.
Let us return to the general case. We now have to construct an elementary abelian
![]() $2$
-extension of degree
$2$
-extension of degree
![]() $2^n$
over L which is an
$2^n$
over L which is an
![]() $F_{2^n}$
-extension over k. We fix a generator g of
$F_{2^n}$
-extension over k. We fix a generator g of
![]() $\mathbb {F}_{2^n}^{\times }$
and consider the
$\mathbb {F}_{2^n}^{\times }$
and consider the
![]() $\mathbb {F}_{2^n}$
-valued characters
$\mathbb {F}_{2^n}$
-valued characters
Here, we consider the cyclic group
![]() $C_{2^n-1}$
as a Galois group of
$C_{2^n-1}$
as a Galois group of
![]() $L/k$
, and
$L/k$
, and
![]() $\sigma $
is a fixed generator of
$\sigma $
is a fixed generator of
![]() $C_{2^n-1}$
. In this situation, it is necessary to distinguish
$C_{2^n-1}$
. In this situation, it is necessary to distinguish
![]() $\operatorname {\mathrm {Gal}} (L/k)$
and
$\operatorname {\mathrm {Gal}} (L/k)$
and
![]() $\mathbb {F}_{2^n}^{\times }$
. We define
$\mathbb {F}_{2^n}^{\times }$
. We define
 $$\begin{align*}e_i = \sum_{j=0}^{2^n-2} \chi_i (\sigma^{-j}) \sigma^j \in \mathbb{F}_{2^n} [C_{2^n-1}]. \end{align*}$$
$$\begin{align*}e_i = \sum_{j=0}^{2^n-2} \chi_i (\sigma^{-j}) \sigma^j \in \mathbb{F}_{2^n} [C_{2^n-1}]. \end{align*}$$
They are the primitive orthogonal idempotents, and we have a direct sum decomposition of the group ring
 $$\begin{align*}\mathbb{F}_{2^n} [C_{2^n-1}] = \bigoplus_{i=0}^{2^n-2} e_i \mathbb{F}_{2^n} [C_{2^n-1}] \end{align*}$$
$$\begin{align*}\mathbb{F}_{2^n} [C_{2^n-1}] = \bigoplus_{i=0}^{2^n-2} e_i \mathbb{F}_{2^n} [C_{2^n-1}] \end{align*}$$
into one-dimensional irreducible modules by Maschke’s theorem.
We now further define
where
![]() $\mathbb {F}_2 (\chi _i)$
is the field generated by the character values of
$\mathbb {F}_2 (\chi _i)$
is the field generated by the character values of
![]() $\chi _i$
. There are as many different
$\chi _i$
. There are as many different
![]() $\varepsilon _i$
as the Galois conjugacy class of the characters
$\varepsilon _i$
as the Galois conjugacy class of the characters
![]() $\{ \chi _i \}$
(see [Reference Isaacs5, Lemma 9.17]), and they are nonzero by [Reference Isaacs5, Corollary 9.22]. If we factor the polynomial
$\{ \chi _i \}$
(see [Reference Isaacs5, Lemma 9.17]), and they are nonzero by [Reference Isaacs5, Corollary 9.22]. If we factor the polynomial
![]() $X^{2^n-1}-1 = \prod _{t} \phi _t (X)$
into irreducibles in the polynomial ring
$X^{2^n-1}-1 = \prod _{t} \phi _t (X)$
into irreducibles in the polynomial ring
![]() $\mathbb {F}_2 [X]$
, then we have a direct sum decomposition over
$\mathbb {F}_2 [X]$
, then we have a direct sum decomposition over
![]() $\mathbb {F}_2$
:
$\mathbb {F}_2$
:
If we choose the index t so that
![]() $\phi _t$
is a minimal polynomial of
$\phi _t$
is a minimal polynomial of
![]() $\chi _t (\sigma )$
, then
$\chi _t (\sigma )$
, then
 $$ \begin{align} \varepsilon_i \mathbb{F}_2 [\sigma ] \cong \bigoplus_{j=0}^{[\mathbb{F}_2 (\chi_i): \mathbb{F}_2]-1} \mathbb{F}_{2^n} [X] /(X- \chi_{ 2^j i} (\sigma)) = \mathbb{F}_2 [X] / (\phi_i (X)). \end{align} $$
$$ \begin{align} \varepsilon_i \mathbb{F}_2 [\sigma ] \cong \bigoplus_{j=0}^{[\mathbb{F}_2 (\chi_i): \mathbb{F}_2]-1} \mathbb{F}_{2^n} [X] /(X- \chi_{ 2^j i} (\sigma)) = \mathbb{F}_2 [X] / (\phi_i (X)). \end{align} $$
Hence, we obtain
Lemma 3.1 Let the notation be as above. If
![]() $(i,2^n-1)=1$
, then the module
$(i,2^n-1)=1$
, then the module
![]() $V_i=\varepsilon _i \mathbb {F}_2 [C_{2^n-1}]$
is an irreducible
$V_i=\varepsilon _i \mathbb {F}_2 [C_{2^n-1}]$
is an irreducible
![]() $\mathbb {F}_2 [C_{2^n-1}]$
-module of dimension n over
$\mathbb {F}_2 [C_{2^n-1}]$
-module of dimension n over
![]() $\mathbb {F}_2$
.
$\mathbb {F}_2$
.
Proof If we assume that
![]() $(i,2^n-1)=1$
, then the order of
$(i,2^n-1)=1$
, then the order of
![]() $\chi _i $
is exactly
$\chi _i $
is exactly
![]() $2^n-1$
and the value of
$2^n-1$
and the value of
![]() $\chi _i$
is not contained in any proper subfields of
$\chi _i$
is not contained in any proper subfields of
![]() $\mathbb {F}_{2^n}$
. Thus, we observe that
$\mathbb {F}_{2^n}$
. Thus, we observe that
![]() $\varepsilon _i \mathbb {F}_2 [C_{2^n-1}]$
is an n-dimensional subspace over
$\varepsilon _i \mathbb {F}_2 [C_{2^n-1}]$
is an n-dimensional subspace over
![]() $\mathbb {F}_2$
.
$\mathbb {F}_2$
.
Since
![]() $\varepsilon _i$
’s are orthogonal idempotents,
$\varepsilon _i$
’s are orthogonal idempotents,
![]() $V_i$
is apparently an
$V_i$
is apparently an
![]() $\mathbb {F}_2 [C_{2^n-1}]$
-module.
$\mathbb {F}_2 [C_{2^n-1}]$
-module.
To show its irreducibility, suppose to the contrary that
![]() $V_i$
is not irreducible. There is a proper submodule W of
$V_i$
is not irreducible. There is a proper submodule W of
![]() $V_i$
. Since
$V_i$
. Since
![]() $V_i$
splits over
$V_i$
splits over
![]() $\mathbb {F}_{2^n}$
, the module W also splits over
$\mathbb {F}_{2^n}$
, the module W also splits over
![]() $\mathbb {F}_{2^n}$
. Therefore, the character of W is a proper subsum of
$\mathbb {F}_{2^n}$
. Therefore, the character of W is a proper subsum of
![]() $\varepsilon _i$
. However, such a subsum does not have its values in
$\varepsilon _i$
. However, such a subsum does not have its values in
![]() $\mathbb {F}_2$
; therefore, W cannot be defined over
$\mathbb {F}_2$
; therefore, W cannot be defined over
![]() $\mathbb {F}_2$
. This is a contradiction.▪
$\mathbb {F}_2$
. This is a contradiction.▪
It is readily seen that there are
![]() $\varphi (2^n-1)/n\ \varepsilon _i$
’s with
$\varphi (2^n-1)/n\ \varepsilon _i$
’s with
![]() $(i,2^n-1)=1$
, where
$(i,2^n-1)=1$
, where
![]() $\varphi $
is the Euler’s totient function.
$\varphi $
is the Euler’s totient function.
Lemma 3.2 Let the notation be as in Lemma
3.1
. If
![]() $(i,2^n-1)=1$
, we have
$(i,2^n-1)=1$
, we have
as abstract groups.
Proof By (1.1), it suffices to show that
![]() $ C_{2^n-1} \ltimes V_i$
is isomorphic to
$ C_{2^n-1} \ltimes V_i$
is isomorphic to
![]() $\mathrm {AGL}_1 (\mathbb {F}_{2^n})$
.
$\mathrm {AGL}_1 (\mathbb {F}_{2^n})$
.
By the isomorphism (3.2), we identify
![]() $V_i $
with
$V_i $
with
![]() $\mathbb {F}_2 [X] / (\phi _i (X))$
, where
$\mathbb {F}_2 [X] / (\phi _i (X))$
, where
![]() $\phi _i (X) $
is the minimal polynomial of
$\phi _i (X) $
is the minimal polynomial of
![]() $g^i = \chi _i (\sigma )$
and hence is of degree n. We define a map
$g^i = \chi _i (\sigma )$
and hence is of degree n. We define a map
![]() $\kappa $
from
$\kappa $
from
![]() $ C_{2^n-1} \ltimes V_i$
to
$ C_{2^n-1} \ltimes V_i$
to
![]() $\mathrm {AGL}_1 (\mathbb {F}_{2^n})$
by
$\mathrm {AGL}_1 (\mathbb {F}_{2^n})$
by
 $$\begin{align*}\kappa \,: \, \left( \sigma^j, U (x) \right) \mapsto \begin{bmatrix} g^{ij} & U (g^i) \\ 0 & 1 \end{bmatrix} \end{align*}$$
$$\begin{align*}\kappa \,: \, \left( \sigma^j, U (x) \right) \mapsto \begin{bmatrix} g^{ij} & U (g^i) \\ 0 & 1 \end{bmatrix} \end{align*}$$
with
![]() $U(X) \in \mathbb {F}_2 [X]$
. By noting that
$U(X) \in \mathbb {F}_2 [X]$
. By noting that
![]() $\sigma $
acts on
$\sigma $
acts on
![]() $V_i$
by the multiplication of g, the map
$V_i$
by the multiplication of g, the map
![]() $\kappa $
sends
$\kappa $
sends
to
 $$\begin{align*}\begin{bmatrix} g^{i(j+\ell)} & \displaystyle U(g^i) + g^{ij} V(g^i) \\ 0 & 1 \end{bmatrix}. \end{align*}$$
$$\begin{align*}\begin{bmatrix} g^{i(j+\ell)} & \displaystyle U(g^i) + g^{ij} V(g^i) \\ 0 & 1 \end{bmatrix}. \end{align*}$$
On the other hand, we compute
 $$\begin{align*}\begin{bmatrix} g^{ij} & U(g^i) \\ 0 & 1 \end{bmatrix} \begin{bmatrix} g^{i\ell} & V(g^i) \\ 0 & 1 \end{bmatrix} = \begin{bmatrix} g^{i(j + \ell ) } & \displaystyle U(g^i) + g^{ij} V(g^i) \\ 0 & 1 \end{bmatrix}. \end{align*}$$
$$\begin{align*}\begin{bmatrix} g^{ij} & U(g^i) \\ 0 & 1 \end{bmatrix} \begin{bmatrix} g^{i\ell} & V(g^i) \\ 0 & 1 \end{bmatrix} = \begin{bmatrix} g^{i(j + \ell ) } & \displaystyle U(g^i) + g^{ij} V(g^i) \\ 0 & 1 \end{bmatrix}. \end{align*}$$
Therefore,
![]() $\kappa $
is a homomorphism.
$\kappa $
is a homomorphism.
We see that
![]() $\left ( \sigma ^j, U(x) \right ) \in \ker \kappa $
if and only if
$\left ( \sigma ^j, U(x) \right ) \in \ker \kappa $
if and only if
![]() $g^{ij} =1$
and
$g^{ij} =1$
and
![]() $ U(g^i) =0 $
. The condition
$ U(g^i) =0 $
. The condition
![]() $g^{ij}=1$
is equivalent to
$g^{ij}=1$
is equivalent to
![]() $j \equiv 0 \pmod {2^n-1}$
since
$j \equiv 0 \pmod {2^n-1}$
since
![]() $(i,2^n-1)=1$
. The condition
$(i,2^n-1)=1$
. The condition
![]() $U(g^i)=1$
is equivalent to the minimal polynomial
$U(g^i)=1$
is equivalent to the minimal polynomial
![]() $\phi _i (X)$
of
$\phi _i (X)$
of
![]() $g^i$
divides
$g^i$
divides
![]() $U(X)$
. Therefore, the kernel consists of the trivial element only. Since the orders of both the groups are the same, the map
$U(X)$
. Therefore, the kernel consists of the trivial element only. Since the orders of both the groups are the same, the map
![]() $\kappa $
is an isomorphism.▪
$\kappa $
is an isomorphism.▪
We can now state our method of construction of
![]() $F_{2^n}$
-extensions.
$F_{2^n}$
-extensions.
Theorem 3.3 Recall that L is a cyclic extension of k of degree
![]() $2^n-1$
and that
$2^n-1$
and that
![]() $\varepsilon _i$
is an idempotent defined by (3.1). Assume that
$\varepsilon _i$
is an idempotent defined by (3.1). Assume that
![]() $(i,2^n-1)=1$
. If
$(i,2^n-1)=1$
. If
![]() $ \theta \in \varepsilon _i \left ( L^{\times }/ (L^{\times })^2 \right )$
is nontrivial, then the Galois closure of
$ \theta \in \varepsilon _i \left ( L^{\times }/ (L^{\times })^2 \right )$
is nontrivial, then the Galois closure of
![]() $L \left ( \sqrt {\theta } \right )$
over k is an
$L \left ( \sqrt {\theta } \right )$
over k is an
![]() $F_{2^n}$
-extension over k.
$F_{2^n}$
-extension over k.
Proof We first note that
![]() $ L^{\times }/ (L^{\times })^2$
is an
$ L^{\times }/ (L^{\times })^2$
is an
![]() $\mathbb {F}_2$
-vector space on which
$\mathbb {F}_2$
-vector space on which
![]() $\operatorname {\mathrm {Gal}} (L/k)$
acts and hence is an
$\operatorname {\mathrm {Gal}} (L/k)$
acts and hence is an
![]() $\mathbb {F}_2 [\operatorname {\mathrm {Gal}} (L/k)]$
-module. Let M be an irreducible
$\mathbb {F}_2 [\operatorname {\mathrm {Gal}} (L/k)]$
-module. Let M be an irreducible
![]() $\mathbb {F}_2 [\operatorname {\mathrm {Gal}} (L/k)]$
-submodule of
$\mathbb {F}_2 [\operatorname {\mathrm {Gal}} (L/k)]$
-submodule of
![]() $L^{\times }/ (L^{\times })^2$
generated by
$L^{\times }/ (L^{\times })^2$
generated by
![]() $\theta $
. By Lemma 3.1, the module M is of dimension n over
$\theta $
. By Lemma 3.1, the module M is of dimension n over
![]() $\mathbb {F}_2$
. Let
$\mathbb {F}_2$
. Let
![]() $(\theta =\theta _1, \ldots , \theta _n)$
be a basis of M. Let K be the field generated by
$(\theta =\theta _1, \ldots , \theta _n)$
be a basis of M. Let K be the field generated by
![]() $\sqrt {\theta _i} \ (i=1,\ldots ,n)$
, that is,
$\sqrt {\theta _i} \ (i=1,\ldots ,n)$
, that is,
![]() $K = L \left ( \sqrt {\theta _1}, \ldots , \sqrt {\theta _n}\right )$
.
$K = L \left ( \sqrt {\theta _1}, \ldots , \sqrt {\theta _n}\right )$
.
We shall first show that K is a Galois extension over k. Let
![]() $\widetilde {\sigma }$
be an extension of
$\widetilde {\sigma }$
be an extension of
![]() $\sigma \in \operatorname {\mathrm {Gal}} (L/k)$
to K. We compute
$\sigma \in \operatorname {\mathrm {Gal}} (L/k)$
to K. We compute
Recalling that M is a multiplicative
![]() $\operatorname {\mathrm {Gal}} (L/k)$
-module, we have
$\operatorname {\mathrm {Gal}} (L/k)$
-module, we have
![]() $\sqrt {\theta '} \in K$
for every element
$\sqrt {\theta '} \in K$
for every element
![]() $\theta ' $
of M. Moreover, in additive notation, there exists
$\theta ' $
of M. Moreover, in additive notation, there exists
![]() $A=[a_{ij}] \in \mathrm {GL}_n (\mathbb {F}_2) $
satisfying
$A=[a_{ij}] \in \mathrm {GL}_n (\mathbb {F}_2) $
satisfying
In particular, we obtain
![]() $\widetilde {\sigma } (\sqrt {\theta _i}) = \pm \sqrt {\sigma (\theta _i)} \in K$
. This shows that
$\widetilde {\sigma } (\sqrt {\theta _i}) = \pm \sqrt {\sigma (\theta _i)} \in K$
. This shows that
![]() $K/ k $
is a Galois extension.
$K/ k $
is a Galois extension.
We have an exact sequence
induced from the restriction map. The Galois group
![]() $\operatorname {\mathrm {Gal}} (L/k )$
acts on
$\operatorname {\mathrm {Gal}} (L/k )$
acts on
![]() $\operatorname {\mathrm {Gal}} (K/L)$
: for
$\operatorname {\mathrm {Gal}} (K/L)$
: for
![]() $\gamma \in \operatorname {\mathrm {Gal}} (K/L)$
and
$\gamma \in \operatorname {\mathrm {Gal}} (K/L)$
and
![]() $\sigma \in \operatorname {\mathrm {Gal}} (L/k)$
, we choose an extension
$\sigma \in \operatorname {\mathrm {Gal}} (L/k)$
, we choose an extension
![]() $\widetilde {\sigma }$
in
$\widetilde {\sigma }$
in
![]() $\operatorname {\mathrm {Gal}} (K/k )$
and we define
$\operatorname {\mathrm {Gal}} (K/k )$
and we define
![]() $\sigma \cdot \gamma = \widetilde {\sigma } \gamma \widetilde {\sigma }^{-1}$
. This action is well defined because
$\sigma \cdot \gamma = \widetilde {\sigma } \gamma \widetilde {\sigma }^{-1}$
. This action is well defined because
![]() $\operatorname {\mathrm {Gal}} (K/L)$
is abelian.
$\operatorname {\mathrm {Gal}} (K/L)$
is abelian.
For
![]() $\sigma \in \operatorname {\mathrm {Gal}} (L/k)$
, we define
$\sigma \in \operatorname {\mathrm {Gal}} (L/k)$
, we define
![]() $s(\sigma ) \in \operatorname {\mathrm {Gal}} (K/k)$
by
$s(\sigma ) \in \operatorname {\mathrm {Gal}} (K/k)$
by
with A defined in (3.3). It is easy to verify that this map s gives a splitting homomorphism and the above exact sequence splits.
By Kummer theory, there exists a bilinear nondegenerate pairing defined as
 $$ \begin{align} \langle \cdot , \cdot \rangle \ : \ \operatorname{\mathrm{Gal}} (K/L) \times M \longrightarrow \mu_2 \longrightarrow \mathbb{F}_2, \quad (\gamma, \theta ) \mapsto \frac{\gamma (\sqrt{\theta})}{\sqrt{\theta}}, \end{align} $$
$$ \begin{align} \langle \cdot , \cdot \rangle \ : \ \operatorname{\mathrm{Gal}} (K/L) \times M \longrightarrow \mu_2 \longrightarrow \mathbb{F}_2, \quad (\gamma, \theta ) \mapsto \frac{\gamma (\sqrt{\theta})}{\sqrt{\theta}}, \end{align} $$
where the map
![]() $\mu _2 \longrightarrow \mathbb {F}_2$
is an isomorphism whose inverse map is
$\mu _2 \longrightarrow \mathbb {F}_2$
is an isomorphism whose inverse map is
![]() $\mathbb {F}_2 \ni x \mapsto (-1)^x$
. This yields an isomorphism
$\mathbb {F}_2 \ni x \mapsto (-1)^x$
. This yields an isomorphism
Both the sides of (3.5) are
![]() $\operatorname {\mathrm {Gal}} (L/k )$
-modules. The action on the right-hand side is given by
$\operatorname {\mathrm {Gal}} (L/k )$
-modules. The action on the right-hand side is given by
![]() $\sigma ( \theta \mapsto \langle \gamma , \theta \rangle ) = ( \theta \mapsto \langle \gamma , \sigma \theta \rangle ) $
.
$\sigma ( \theta \mapsto \langle \gamma , \theta \rangle ) = ( \theta \mapsto \langle \gamma , \sigma \theta \rangle ) $
.
We shall show that
![]() $\operatorname {\mathrm {Gal}} (K/L)$
is an irreducible
$\operatorname {\mathrm {Gal}} (K/L)$
is an irreducible
![]() $\mathbb {F}_2 [\operatorname {\mathrm {Gal}} (L/k )]$
-module isomorphic to
$\mathbb {F}_2 [\operatorname {\mathrm {Gal}} (L/k )]$
-module isomorphic to
![]() $\varepsilon _j \mathbb {F}_2 [\operatorname {\mathrm {Gal}} (L/k )]$
for some integer j prime to
$\varepsilon _j \mathbb {F}_2 [\operatorname {\mathrm {Gal}} (L/k )]$
for some integer j prime to
![]() $2^n-1$
. Then, from Lemma 3.2,
$2^n-1$
. Then, from Lemma 3.2,
![]() $\operatorname {\mathrm {Gal}} (K/k) \cong F_{2^n}$
follows. To do this end, we compute the action of
$\operatorname {\mathrm {Gal}} (K/k) \cong F_{2^n}$
follows. To do this end, we compute the action of
![]() $\sigma \in \operatorname {\mathrm {Gal}} (L/k)$
on
$\sigma \in \operatorname {\mathrm {Gal}} (L/k)$
on
![]() $\operatorname {\mathrm {Gal}} (K/L)$
in terms of (3.3). In the above, we have shown that
$\operatorname {\mathrm {Gal}} (K/L)$
in terms of (3.3). In the above, we have shown that
![]() $\widetilde {\sigma }(\sqrt {\theta _i}) = \pm \sqrt {\sigma \theta _i}$
, and thus we can define
$\widetilde {\sigma }(\sqrt {\theta _i}) = \pm \sqrt {\sigma \theta _i}$
, and thus we can define
![]() $e_i \in \mathbb {F}_2$
by
$e_i \in \mathbb {F}_2$
by
Using (3.3), we can compute further
 $$\begin{align*}\widetilde{\sigma } (\sqrt{\theta_i}) = (-1)^{e_i} \prod_{j=1}^n \sqrt{\theta_j}^{a_{ji}}. \end{align*}$$
$$\begin{align*}\widetilde{\sigma } (\sqrt{\theta_i}) = (-1)^{e_i} \prod_{j=1}^n \sqrt{\theta_j}^{a_{ji}}. \end{align*}$$
By writing
![]() $A^{-1} = [b_{ij}]$
, we have
$A^{-1} = [b_{ij}]$
, we have
 $$\begin{align*}\widetilde{\sigma }^{-1} \sqrt{\theta_i} = (-1)^{f_i} \sqrt{\sigma^{-1} \theta_i} = (-1)^{f_i} \prod_{j=1}^n \sqrt{\theta_j}^{b_{ji}} \end{align*}$$
$$\begin{align*}\widetilde{\sigma }^{-1} \sqrt{\theta_i} = (-1)^{f_i} \sqrt{\sigma^{-1} \theta_i} = (-1)^{f_i} \prod_{j=1}^n \sqrt{\theta_j}^{b_{ji}} \end{align*}$$
with some
![]() $f_i \in \mathbb {F}_2$
. The relation of
$f_i \in \mathbb {F}_2$
. The relation of
![]() $e_i$
’s and
$e_i$
’s and
![]() $f_i$
’s is derived by computing
$f_i$
’s is derived by computing
![]() $\widetilde {\sigma } \, \widetilde {\sigma }^{-1} \left ( \sqrt {\theta _i} \right ) = \sqrt {\theta _i}$
. In fact, the left-hand side is equal to
$\widetilde {\sigma } \, \widetilde {\sigma }^{-1} \left ( \sqrt {\theta _i} \right ) = \sqrt {\theta _i}$
. In fact, the left-hand side is equal to
 $$\begin{align*}(-1)^{f_i} \widetilde{\sigma} \left( \prod_{j=1}^n \sqrt{\theta_j}^{b_{ji}} \right) = (-1)^{f_i} \prod_{j=1}^n (-1)^{e_j b_{ji}} \left( \prod_{k=1}^n \sqrt{\theta_j}^{a_{kj}} \right)^{b_{ji}} = (-1)^{f_i+ \sum_{j=1}^n e_j b_{ji} } \sqrt{\theta_i}. \end{align*}$$
$$\begin{align*}(-1)^{f_i} \widetilde{\sigma} \left( \prod_{j=1}^n \sqrt{\theta_j}^{b_{ji}} \right) = (-1)^{f_i} \prod_{j=1}^n (-1)^{e_j b_{ji}} \left( \prod_{k=1}^n \sqrt{\theta_j}^{a_{kj}} \right)^{b_{ji}} = (-1)^{f_i+ \sum_{j=1}^n e_j b_{ji} } \sqrt{\theta_i}. \end{align*}$$
Hence, we obtain
 $$ \begin{align} f_i+ \sum_{j=1}^n e_j b_{ji} =0 \text{ for all } i=1, \ldots , n. \end{align} $$
$$ \begin{align} f_i+ \sum_{j=1}^n e_j b_{ji} =0 \text{ for all } i=1, \ldots , n. \end{align} $$
Now, let
![]() $(g_1, \ldots , g_n)$
be the dual basis of
$(g_1, \ldots , g_n)$
be the dual basis of
![]() $\operatorname {\mathrm {Gal}} (K/L)$
with respect to the paring
$\operatorname {\mathrm {Gal}} (K/L)$
with respect to the paring
![]() $\langle \cdot , \cdot \rangle $
. We compute the action
$\langle \cdot , \cdot \rangle $
. We compute the action
![]() $\sigma \cdot g_i$
on
$\sigma \cdot g_i$
on
![]() $\sqrt {\theta _j}:$
$\sqrt {\theta _j}:$
 $$ \begin{align*} (\sigma \cdot g_i) \left( \sqrt{\theta_j} \right) &= \widetilde{\sigma} g_i \widetilde{\sigma}^{-1} \left( \sqrt{\theta_j} \right) = \widetilde{\sigma} g_i \left( (-1)^{f_j} \prod_{k=1}^n \sqrt{\theta_k}^{b_{kj}}\right) \\[6pt] &= (-1)^{f_j} \widetilde{\sigma} \left( (-1)^{b_{ij}} \prod_{k=1}^n \sqrt{\theta_k}^{b_{kj}}\right) = (-1)^{f_j + b_{ij}} \prod_{k=1}^n \left( \widetilde{\sigma} \sqrt{\theta_k}\right)^{b_{kj}} \\[6pt] &= (-1)^{f_j + b_{ij} + \sum_{k=1}^n e_k b_{kj}} \sqrt{\theta_j}. \end{align*} $$
$$ \begin{align*} (\sigma \cdot g_i) \left( \sqrt{\theta_j} \right) &= \widetilde{\sigma} g_i \widetilde{\sigma}^{-1} \left( \sqrt{\theta_j} \right) = \widetilde{\sigma} g_i \left( (-1)^{f_j} \prod_{k=1}^n \sqrt{\theta_k}^{b_{kj}}\right) \\[6pt] &= (-1)^{f_j} \widetilde{\sigma} \left( (-1)^{b_{ij}} \prod_{k=1}^n \sqrt{\theta_k}^{b_{kj}}\right) = (-1)^{f_j + b_{ij}} \prod_{k=1}^n \left( \widetilde{\sigma} \sqrt{\theta_k}\right)^{b_{kj}} \\[6pt] &= (-1)^{f_j + b_{ij} + \sum_{k=1}^n e_k b_{kj}} \sqrt{\theta_j}. \end{align*} $$
Combining with (3.6), we have
This means that
![]() $\sigma $
acts on
$\sigma $
acts on
![]() $\operatorname {\mathrm {Gal}} (K/L)$
by
$\operatorname {\mathrm {Gal}} (K/L)$
by
![]() $A^{-1}$
. Therefore,
$A^{-1}$
. Therefore,
![]() $\operatorname {\mathrm {Gal}} (K/L)$
is isomorphic to an irreducible module
$\operatorname {\mathrm {Gal}} (K/L)$
is isomorphic to an irreducible module
![]() $\varepsilon _{-i} \mathbb {F}_2 [\operatorname {\mathrm {Gal}} (L/k )]$
. Since
$\varepsilon _{-i} \mathbb {F}_2 [\operatorname {\mathrm {Gal}} (L/k )]$
. Since
![]() $(-i, 2^n-1) =1$
, we conclude
$(-i, 2^n-1) =1$
, we conclude
![]() ${\operatorname {\mathrm {Gal}} (K/k) \cong F_{2^n}}$
.
${\operatorname {\mathrm {Gal}} (K/k) \cong F_{2^n}}$
.
This completes the proof of Theorem 3.3.▪
Remark 3.4 Our proof shows that if
![]() $\sigma $
acts on M by A as (3.3), then it acts on
$\sigma $
acts on M by A as (3.3), then it acts on
![]() $\operatorname {\mathrm {Gal}} (K/L)$
by
$\operatorname {\mathrm {Gal}} (K/L)$
by
![]() $A^{-1}$
. This argument does not depend on the assumption that
$A^{-1}$
. This argument does not depend on the assumption that
![]() ${(i,2^n-1)=1}$
. If we drop this assumption, then we obtain Galois extensions whose Galois groups are various semidirect products of
${(i,2^n-1)=1}$
. If we drop this assumption, then we obtain Galois extensions whose Galois groups are various semidirect products of
![]() $\operatorname {\mathrm {Gal}} (L/k)$
and
$\operatorname {\mathrm {Gal}} (L/k)$
and
![]() $\operatorname {\mathrm {Gal}} (K/L)$
including the direct product. See [Reference Kida7, Section 6] for example.
$\operatorname {\mathrm {Gal}} (K/L)$
including the direct product. See [Reference Kida7, Section 6] for example.
The following corollary follows from the proof of Theorem 3.3.
Corollary 3.5 With the same assumptions as in Theorem
3.3
, the Galois closure of
![]() $L \left ( \sqrt {\theta } \right )$
over k is
$L \left ( \sqrt {\theta } \right )$
over k is
![]() $L \left ( \sqrt {\sigma \theta } \mid \sigma \in \operatorname {\mathrm {Gal}} (L/k) \right )$
.
$L \left ( \sqrt {\sigma \theta } \mid \sigma \in \operatorname {\mathrm {Gal}} (L/k) \right )$
.
The following corollary guarantees that there are infinitely many
![]() $F_{2^n}$
-extensions containing L.
$F_{2^n}$
-extensions containing L.
Corollary 3.6 Let
![]() $\theta $
and
$\theta $
and
![]() $\theta '$
be nontrivial elements in
$\theta '$
be nontrivial elements in
![]() $\varepsilon _i (L^{\times }/ (L^{\times })^2)$
for some i. The Galois closures of
$\varepsilon _i (L^{\times }/ (L^{\times })^2)$
for some i. The Galois closures of
![]() $L (\sqrt {\theta })$
and
$L (\sqrt {\theta })$
and
![]() $L(\sqrt {\theta '})$
coincide if and only if the
$L(\sqrt {\theta '})$
coincide if and only if the
![]() $\operatorname {\mathrm {Gal}} (L/k)$
-modules generated, respectively, by
$\operatorname {\mathrm {Gal}} (L/k)$
-modules generated, respectively, by
![]() $\theta $
and
$\theta $
and
![]() $\theta '$
coincide.
$\theta '$
coincide.
Proof This follows from the Kummer duality (3.4).▪
4 Identifying arithmetically equivalent fields
In the previous section, we have constructed
![]() $F_{2^n}$
-extensions. In this section, we explain how to identify arithmetically equivalent fields inside the
$F_{2^n}$
-extensions. In this section, we explain how to identify arithmetically equivalent fields inside the
![]() $F_{2^n}$
-extensions.
$F_{2^n}$
-extensions.
We continue to use the notation used in the proof of Theorem 3.3. For convenience, we recall some of them. Let
![]() $L/k$
be a cyclic extension of degree
$L/k$
be a cyclic extension of degree
![]() $2^n-1$
. We assume that i is an integer prime to
$2^n-1$
. We assume that i is an integer prime to
![]() $2^n-1$
and consider an irreducible
$2^n-1$
and consider an irreducible
![]() $\mathbb {F}_2 [\operatorname {\mathrm {Gal}} (L/k)]$
-module M in
$\mathbb {F}_2 [\operatorname {\mathrm {Gal}} (L/k)]$
-module M in
![]() $ \varepsilon _i\left ( L^{\times }/ (L^{\times })^2 \right )$
, where
$ \varepsilon _i\left ( L^{\times }/ (L^{\times })^2 \right )$
, where
![]() $\varepsilon _i$
is the idempotent defined by (3.1). The module M is generated by
$\varepsilon _i$
is the idempotent defined by (3.1). The module M is generated by
![]() $\theta $
and has a basis
$\theta $
and has a basis
![]() $(\theta =\theta _1, \ldots , \theta _n)$
over
$(\theta =\theta _1, \ldots , \theta _n)$
over
![]() $\mathbb {F}_2$
. We now fix a generator
$\mathbb {F}_2$
. We now fix a generator
![]() $\sigma $
of
$\sigma $
of
![]() $\operatorname {\mathrm {Gal}} (L/k)$
and assume that
$\operatorname {\mathrm {Gal}} (L/k)$
and assume that
![]() $\sigma $
acts on the above basis by (3.3). The Galois group
$\sigma $
acts on the above basis by (3.3). The Galois group
![]() $\operatorname {\mathrm {Gal}} (K/L)$
is isomorphic to the dual group
$\operatorname {\mathrm {Gal}} (K/L)$
is isomorphic to the dual group
![]() $\mathrm {Hom} ( M, \mathbb {F}_2)$
of M (see (3.5)). We want to find quadratic extensions of
$\mathrm {Hom} ( M, \mathbb {F}_2)$
of M (see (3.5)). We want to find quadratic extensions of
![]() $L (\sqrt {\theta })$
which are arithmetically equivalent but not conjugate. In Proposition 2.1, we have shown that all such quadratic extensions are arithmetically equivalent, and hence we only have to identify the conjugacy classes of these fields.
$L (\sqrt {\theta })$
which are arithmetically equivalent but not conjugate. In Proposition 2.1, we have shown that all such quadratic extensions are arithmetically equivalent, and hence we only have to identify the conjugacy classes of these fields.
Definition 4.1 We denote by
![]() $\widetilde {\mathbb {F}_2^n}$
the quotient space of
$\widetilde {\mathbb {F}_2^n}$
the quotient space of
![]() $\mathbb {F}_2^n$
by the subspace generated by
$\mathbb {F}_2^n$
by the subspace generated by
![]() $\boldsymbol {e}_1= {}^t (1,0,\ldots ,0 )$
. Namely, column vectors
$\boldsymbol {e}_1= {}^t (1,0,\ldots ,0 )$
. Namely, column vectors
![]() $\boldsymbol {e}$
and
$\boldsymbol {e}$
and
![]() $\boldsymbol {f} \in \mathbb {F}_2^n$
are equal in
$\boldsymbol {f} \in \mathbb {F}_2^n$
are equal in
![]() $\widetilde {\mathbb {F}_2^n}$
if they coincide except for the first coordinate.
$\widetilde {\mathbb {F}_2^n}$
if they coincide except for the first coordinate.
If
![]() $\tilde {\boldsymbol {v}} = {}^t (e_1, \ldots , e_n ) \in \widetilde {\mathbb {F}_2^{n}}$
, then a quadratic extension
$\tilde {\boldsymbol {v}} = {}^t (e_1, \ldots , e_n ) \in \widetilde {\mathbb {F}_2^{n}}$
, then a quadratic extension
of
![]() $L \left ( \sqrt {\theta } \right )$
is well defined and there is a one-to-one correspondence between such quadratic extensions and the set
$L \left ( \sqrt {\theta } \right )$
is well defined and there is a one-to-one correspondence between such quadratic extensions and the set
![]() $\widetilde {\mathbb {F}_2^{n}} - \{ \tilde {\boldsymbol {0}}\}$
. The conjugate field of
$\widetilde {\mathbb {F}_2^{n}} - \{ \tilde {\boldsymbol {0}}\}$
. The conjugate field of
![]() $ Q (\tilde {\boldsymbol {v}})$
by
$ Q (\tilde {\boldsymbol {v}})$
by
![]() $\sigma $
is then given by
$\sigma $
is then given by
 $$\begin{align*}\sigma Q (\tilde{\boldsymbol{v}}) = L \left( \prod_{k=1}^n \sqrt{\theta_k^{~a_{k1}}}, \prod_{k=1}^n \sqrt{\theta_k^{~e_2 a_{k2} + \cdots + e_n a_{kn}}} \right) \end{align*}$$
$$\begin{align*}\sigma Q (\tilde{\boldsymbol{v}}) = L \left( \prod_{k=1}^n \sqrt{\theta_k^{~a_{k1}}}, \prod_{k=1}^n \sqrt{\theta_k^{~e_2 a_{k2} + \cdots + e_n a_{kn}}} \right) \end{align*}$$
with
![]() $A=[a_{ij}]$
in (3.3). The condition for
$A=[a_{ij}]$
in (3.3). The condition for
![]() $\sigma Q (\tilde {\boldsymbol {v}}) \supset L (\sqrt {\theta })$
is equivalent to that
$\sigma Q (\tilde {\boldsymbol {v}}) \supset L (\sqrt {\theta })$
is equivalent to that
![]() $\theta _1$
coincides with either
$\theta _1$
coincides with either
![]() $\prod _{k=1}^n \theta _k^{~e_2 a_{k2} + \cdots + e_n a_{kn}} $
or the product
$\prod _{k=1}^n \theta _k^{~e_2 a_{k2} + \cdots + e_n a_{kn}} $
or the product
![]() $\prod _{k=1}^n {\theta _k^{~a_{k1}+ e_2 a_{k2} + \cdots + e_n a_{kn}}} $
since
$\prod _{k=1}^n {\theta _k^{~a_{k1}+ e_2 a_{k2} + \cdots + e_n a_{kn}}} $
since
![]() $\prod _{k=1}^n \theta _k^{a_{k1}}$
does not coincide with
$\prod _{k=1}^n \theta _k^{a_{k1}}$
does not coincide with
![]() $\theta _1$
. It is easy to observe that this condition holds if and only if
$\theta _1$
. It is easy to observe that this condition holds if and only if
![]() $A \tilde {\boldsymbol {v}} = \boldsymbol {e}_1 $
. If
$A \tilde {\boldsymbol {v}} = \boldsymbol {e}_1 $
. If
![]() $\tilde {\boldsymbol {v}}$
satisfies this condition, then
$\tilde {\boldsymbol {v}}$
satisfies this condition, then
![]() $Q (\tilde {\boldsymbol {v}}) = Q (A^{-1} \boldsymbol {e}_1) $
is conjugate to
$Q (\tilde {\boldsymbol {v}}) = Q (A^{-1} \boldsymbol {e}_1) $
is conjugate to
![]() $ Q (A \boldsymbol {e}_1) $
. Note that since
$ Q (A \boldsymbol {e}_1) $
. Note that since
![]() $\operatorname {\mathrm {Gal}} (L/k)$
acts transitively on
$\operatorname {\mathrm {Gal}} (L/k)$
acts transitively on
![]() $\widetilde {\mathbb {F}_2^n}$
, for every element
$\widetilde {\mathbb {F}_2^n}$
, for every element
![]() $\tilde {\boldsymbol {v}} \in \widetilde {\mathbb {F}_2^n}$
, there exists an integer j such that
$\tilde {\boldsymbol {v}} \in \widetilde {\mathbb {F}_2^n}$
, there exists an integer j such that
![]() $\tilde {\boldsymbol {v}} = A^j \boldsymbol {e}_1$
.
$\tilde {\boldsymbol {v}} = A^j \boldsymbol {e}_1$
.
In accordance with this observation, we define the following equivalence relation on
![]() $\widetilde {\mathbb {F}_2^n}$
.
$\widetilde {\mathbb {F}_2^n}$
.
Definition 4.2 Let us fix
![]() $\sigma $
as a generator of
$\sigma $
as a generator of
![]() $\operatorname {\mathrm {Gal}} (L/k)$
, and let A be the matrix defined by (3.3). The elements
$\operatorname {\mathrm {Gal}} (L/k)$
, and let A be the matrix defined by (3.3). The elements
![]() $\tilde {\boldsymbol {v}} = A^i \boldsymbol {e}_1$
and
$\tilde {\boldsymbol {v}} = A^i \boldsymbol {e}_1$
and
![]() $\tilde {\boldsymbol {f}} = A^j \boldsymbol {e}_1$
in
$\tilde {\boldsymbol {f}} = A^j \boldsymbol {e}_1$
in
![]() $\widetilde {\mathbb {F}_2^n}$
are said to be equivalent if
$\widetilde {\mathbb {F}_2^n}$
are said to be equivalent if
![]() $i+j \equiv 0 \pmod {2^n-1}$
.
$i+j \equiv 0 \pmod {2^n-1}$
.
Using these definitions, we obtain the following proposition.
Proposition 4.1 Let
![]() $\widetilde {\mathbb {F}_2^n}$
be the set defined by Definition
4.1
. The map sending
$\widetilde {\mathbb {F}_2^n}$
be the set defined by Definition
4.1
. The map sending
![]() $\tilde {\boldsymbol {v}} \in \widetilde {\mathbb {F}_2^{n}}$
to
$\tilde {\boldsymbol {v}} \in \widetilde {\mathbb {F}_2^{n}}$
to
![]() $Q (\tilde {\boldsymbol {v}})$
as in (4.1) induces a one-to-one correspondence between the conjugacy classes over k of quadratic extensions over
$Q (\tilde {\boldsymbol {v}})$
as in (4.1) induces a one-to-one correspondence between the conjugacy classes over k of quadratic extensions over
![]() $L (\sqrt {\theta })$
and the equivalence classes of
$L (\sqrt {\theta })$
and the equivalence classes of
![]() $\widetilde {\mathbb {F}_2^n} -\{ \tilde {\boldsymbol {0}}\}$
by the equivalence relation in Definition
4.2
.
$\widetilde {\mathbb {F}_2^n} -\{ \tilde {\boldsymbol {0}}\}$
by the equivalence relation in Definition
4.2
.
For explicit computation, it remains to give a basis of the irreducible module
![]() $M=\langle \theta \rangle $
. We use the isomorphism
$M=\langle \theta \rangle $
. We use the isomorphism
in (3.2) for that purpose. Recall that
![]() $\phi _i (X)$
is the minimal polynomial of
$\phi _i (X)$
is the minimal polynomial of
![]() $g^i$
over
$g^i$
over
![]() $\mathbb {F}_2$
, where g is a fixed generator of
$\mathbb {F}_2$
, where g is a fixed generator of
![]() $\mathbb {F}_{2^n}^{\times }$
, and that
$\mathbb {F}_{2^n}^{\times }$
, and that
![]() $\sigma \in \operatorname {\mathrm {Gal}} (L/k)$
acts on the right-hand side by the multiplication by X. Thus, if we take
$\sigma \in \operatorname {\mathrm {Gal}} (L/k)$
acts on the right-hand side by the multiplication by X. Thus, if we take
![]() $(1,X, \ldots , X^{n-1})$
as a basis of
$(1,X, \ldots , X^{n-1})$
as a basis of
![]() $\mathbb {F}_2 [X]/(\phi _i (X))$
, then
$\mathbb {F}_2 [X]/(\phi _i (X))$
, then
![]() $\sigma $
acts by the companion matrix of
$\sigma $
acts by the companion matrix of
![]() $\phi _i (X) = a_0 +a_1 X + \cdots + a_{n-1}X^{n-1} + X^n :$
$\phi _i (X) = a_0 +a_1 X + \cdots + a_{n-1}X^{n-1} + X^n :$
 $$\begin{align*}\begin{bmatrix} 0 & 0 & & & & a_0 \\ 1& 0 & & & & a_1 \\ 0&1 & \ddots & & & a_2 \\ \vdots & & \ddots & \ddots & & \vdots \\ & & & \ddots & 0 & a_{n-2} \\ 0 & & & \cdots &1 & a_{n-1} \end{bmatrix}. \end{align*}$$
$$\begin{align*}\begin{bmatrix} 0 & 0 & & & & a_0 \\ 1& 0 & & & & a_1 \\ 0&1 & \ddots & & & a_2 \\ \vdots & & \ddots & \ddots & & \vdots \\ & & & \ddots & 0 & a_{n-2} \\ 0 & & & \cdots &1 & a_{n-1} \end{bmatrix}. \end{align*}$$
This matrix action is compatible if we take a basis
![]() $(\theta ,\sigma \theta , \ldots , \sigma ^{n-1} \theta )$
for M.
$(\theta ,\sigma \theta , \ldots , \sigma ^{n-1} \theta )$
for M.
To illustrate how the above method works, we give an explicit description for the case
![]() $n=4$
.
$n=4$
.
Proposition 4.2 Let L be a cyclic extension of
![]() $\mathbb {Q}$
of degree
$\mathbb {Q}$
of degree
![]() $15$
with Galois group generated by
$15$
with Galois group generated by
![]() $ \sigma $
. If
$ \sigma $
. If
![]() $\theta $
is a nontrivial element of
$\theta $
is a nontrivial element of
![]() $\varepsilon _1 (L^{\times }/ (L^{\times })^2)$
, then three fields
$\varepsilon _1 (L^{\times }/ (L^{\times })^2)$
, then three fields
are not conjugate but arithmetically equivalent.
Proof We consider an irreducible module
![]() $M= (\theta , \sigma \theta , \sigma ^2 \theta , \sigma ^3 \theta )$
, which is isomorphic to
$M= (\theta , \sigma \theta , \sigma ^2 \theta , \sigma ^3 \theta )$
, which is isomorphic to
![]() $\mathbb {F}_2 [X] / \phi _1 (X) =\mathbb {F}_2 [X] /(X^4+X+1)$
. Hence, the action of
$\mathbb {F}_2 [X] / \phi _1 (X) =\mathbb {F}_2 [X] /(X^4+X+1)$
. Hence, the action of
![]() $\sigma $
is given by the companion matrix A of
$\sigma $
is given by the companion matrix A of
![]() $\phi _1 (X)$
:
$\phi _1 (X)$
:
 $$\begin{align*}\sigma (\theta, \sigma (\theta), \sigma^2 (\theta ) , \sigma^3 (\theta)) = (\theta, \sigma (\theta), \sigma^2 (\theta ) , \sigma^3 (\theta)) \begin{bmatrix} 0 & 0 & 0 & 1 \\ 1 &0 &0 & 1 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix}. \end{align*}$$
$$\begin{align*}\sigma (\theta, \sigma (\theta), \sigma^2 (\theta ) , \sigma^3 (\theta)) = (\theta, \sigma (\theta), \sigma^2 (\theta ) , \sigma^3 (\theta)) \begin{bmatrix} 0 & 0 & 0 & 1 \\ 1 &0 &0 & 1 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix}. \end{align*}$$
Let
![]() $\boldsymbol {v}_i =A^i \boldsymbol {e}_1$
for
$\boldsymbol {v}_i =A^i \boldsymbol {e}_1$
for
![]() $i=0,\ldots , 14$
. If we denote the element in
$i=0,\ldots , 14$
. If we denote the element in
![]() $\widetilde {\mathbb {F}_2^{4}}$
corresponding to
$\widetilde {\mathbb {F}_2^{4}}$
corresponding to
![]() $\boldsymbol {v}_i$
by
$\boldsymbol {v}_i$
by
![]() $\tilde {\boldsymbol {v}}_i$
, then the equivalence classes by Definition 4.1 are easily computed, and we have
$\tilde {\boldsymbol {v}}_i$
, then the equivalence classes by Definition 4.1 are easily computed, and we have
We further connect them by the equivalence relation in Definition 4.2:
By combining these, it follows that the conjugacy classes of the quadratic extensions of
![]() $L (\sqrt {\theta })$
in K are
$L (\sqrt {\theta })$
in K are
 $$ \begin{align*} & \{ Q (\tilde{\boldsymbol{v}}_1), Q (\tilde{\boldsymbol{v}}_3), Q (\tilde{\boldsymbol{v}}_{11}) \}, \\[3pt] & \{ Q (\tilde{\boldsymbol{v}}_2), Q (\tilde{\boldsymbol{v}}_6), Q (\tilde{\boldsymbol{v}}_{9}) \}, \\[3pt] & \{ Q (\tilde{\boldsymbol{v}}_5) \}. \end{align*} $$
$$ \begin{align*} & \{ Q (\tilde{\boldsymbol{v}}_1), Q (\tilde{\boldsymbol{v}}_3), Q (\tilde{\boldsymbol{v}}_{11}) \}, \\[3pt] & \{ Q (\tilde{\boldsymbol{v}}_2), Q (\tilde{\boldsymbol{v}}_6), Q (\tilde{\boldsymbol{v}}_{9}) \}, \\[3pt] & \{ Q (\tilde{\boldsymbol{v}}_5) \}. \end{align*} $$
Therefore, we can choose
![]() $Q (\tilde {\boldsymbol {v}}_1)$
,
$Q (\tilde {\boldsymbol {v}}_1)$
,
![]() $Q (\tilde {\boldsymbol {v}}_2)$
,
$Q (\tilde {\boldsymbol {v}}_2)$
,
![]() $Q (\tilde {\boldsymbol {v}}_5)$
as representatives of the conjugacy classes. These fields are nothing but ones in the statement of the proposition.▪
$Q (\tilde {\boldsymbol {v}}_5)$
as representatives of the conjugacy classes. These fields are nothing but ones in the statement of the proposition.▪
We give a numerical example of Proposition 4.2 using Magma [Reference Bosma, Cannon and Playoust2].
Example 4.3 Let L be a unique cyclic extension of degree
![]() $15$
inside the
$15$
inside the
![]() $31$
st cyclotomic field. A defining polynomial of L is
$31$
st cyclotomic field. A defining polynomial of L is
 $$ \begin{align*} f(X) &= X^{15}-31 X^{14}+434 X^{13}-3,627 X^{12}+20,150 X^{11}-78,430 X^{10} \\ &\quad +219,604 X^{9}-447,051 X^{8}+660,858 X^{7}-700,910 X^{6}+520,676 X^{5} \\& \quad -260,338 X^{4} +82,212 X^{3}-14,756 X^{2}+1,240 X-31 \in \mathbb{Q} [X]. \end{align*} $$
$$ \begin{align*} f(X) &= X^{15}-31 X^{14}+434 X^{13}-3,627 X^{12}+20,150 X^{11}-78,430 X^{10} \\ &\quad +219,604 X^{9}-447,051 X^{8}+660,858 X^{7}-700,910 X^{6}+520,676 X^{5} \\& \quad -260,338 X^{4} +82,212 X^{3}-14,756 X^{2}+1,240 X-31 \in \mathbb{Q} [X]. \end{align*} $$
Let
![]() $\alpha $
be a root of f and
$\alpha $
be a root of f and
![]() $\sigma $
a generator of
$\sigma $
a generator of
![]() $\operatorname {\mathrm {Gal}} (L/\mathbb {Q})$
sending
$\operatorname {\mathrm {Gal}} (L/\mathbb {Q})$
sending
![]() $\alpha $
to
$\alpha $
to
![]() $\alpha ^3-6\alpha ^2 + 9 \alpha $
. We have
$\alpha ^3-6\alpha ^2 + 9 \alpha $
. We have
Unfortunately, we have
![]() $\varepsilon _1 (\alpha ) \in (L^{\times })^2$
, and we instead take
$\varepsilon _1 (\alpha ) \in (L^{\times })^2$
, and we instead take
![]() $\theta = \varepsilon _1 (\alpha +1 ) $
, which is nontrivial:
$\theta = \varepsilon _1 (\alpha +1 ) $
, which is nontrivial:
 $$ \begin{align*} \theta &= 1,918 \alpha^{14} - 55,941 \alpha^{13} + 730,762 \alpha^{12} - 5,642,195 \alpha^{11} + 28,615,030 \alpha^{10} \\ &\quad - 100,198,470 \alpha^9 + 247,832,148 \alpha^8 - 435,429,135 \alpha^7 + 538,848,977 \alpha^6 \\ &\quad - 459,012,245 \alpha^5 + 258,286,255 \alpha^4 - 89,753,523 \alpha^3 + 17,269,217 \alpha^2 \\&\quad - 1,514,740 \alpha + 41,200. \end{align*} $$
$$ \begin{align*} \theta &= 1,918 \alpha^{14} - 55,941 \alpha^{13} + 730,762 \alpha^{12} - 5,642,195 \alpha^{11} + 28,615,030 \alpha^{10} \\ &\quad - 100,198,470 \alpha^9 + 247,832,148 \alpha^8 - 435,429,135 \alpha^7 + 538,848,977 \alpha^6 \\ &\quad - 459,012,245 \alpha^5 + 258,286,255 \alpha^4 - 89,753,523 \alpha^3 + 17,269,217 \alpha^2 \\&\quad - 1,514,740 \alpha + 41,200. \end{align*} $$
The Galois closure K of
![]() $L (\sqrt {\theta })$
is isomorphic to
$L (\sqrt {\theta })$
is isomorphic to
![]() $F_{2^4}$
as expected.
$F_{2^4}$
as expected.
The arithmetically equivalent fields in Proposition 4.2 are generated, respectively, by
 $$ \begin{align*} \sigma \theta = & -1,868 \alpha^{14} + 51,883 \alpha^{13} - 644,123 \alpha^{12} + 4,716,495 \alpha^{11} - 22,632,746 \alpha^{10} \\ & + 74,787,369 \alpha^{9} - 174,015,255 \alpha^{8} + 286,515,188 \alpha^{7} - 330,720,046 \alpha^{6} \\ & + 261,327,388 \alpha^{5} - 135,654,656 \alpha^{4} + 43,411,399 \alpha^{3} - 7,829,444 \alpha^{2} \\& + 707,661 \alpha - 16,708, \\ \sigma^{2} \theta = &568 \alpha^{14} - 14,474 \alpha^{13} + 159,857 \alpha^{12} - 991,986 \alpha^{11} + 3,704,900 \alpha^{10} \\ & - 7,937,152 \alpha^{9} + 6,068,083 \alpha^{8} + 15,337,953 \alpha^{7} - 53,985,594 \alpha^{6} \\ & + 78,016,586 \alpha^{5} - 62,566,399 \alpha^{4} + 27,793,973 \alpha^{3} - 6,084,932 \alpha^{2} \\ & + 495,906 \alpha + 900, \nonumber \\\sigma \theta \cdot \sigma^{2} \theta = & -2,171,688 \alpha^{14} + 67,084,221 \alpha^{13} - 934,645,093 \alpha^{12} + 7,750,575,584 \alpha^{11} \\ & - 42,508,235,392 \alpha^{10} + 162,029,379,062 \alpha^{9} - 438,947,076,273 \alpha^{8} \\ & + 849,307,812,685 \alpha^{7} - 1,162,572,370,875 \alpha^{6} + 1,098,352,512,421 \alpha^{5} \\& - 685,146,475,599 \alpha^{4} + 262,216,335,852 \alpha^{3} - 54,652,878,964 \alpha^{2} \\& + 5,143,605,707 \alpha - 112,645,567. \end{align*} $$
$$ \begin{align*} \sigma \theta = & -1,868 \alpha^{14} + 51,883 \alpha^{13} - 644,123 \alpha^{12} + 4,716,495 \alpha^{11} - 22,632,746 \alpha^{10} \\ & + 74,787,369 \alpha^{9} - 174,015,255 \alpha^{8} + 286,515,188 \alpha^{7} - 330,720,046 \alpha^{6} \\ & + 261,327,388 \alpha^{5} - 135,654,656 \alpha^{4} + 43,411,399 \alpha^{3} - 7,829,444 \alpha^{2} \\& + 707,661 \alpha - 16,708, \\ \sigma^{2} \theta = &568 \alpha^{14} - 14,474 \alpha^{13} + 159,857 \alpha^{12} - 991,986 \alpha^{11} + 3,704,900 \alpha^{10} \\ & - 7,937,152 \alpha^{9} + 6,068,083 \alpha^{8} + 15,337,953 \alpha^{7} - 53,985,594 \alpha^{6} \\ & + 78,016,586 \alpha^{5} - 62,566,399 \alpha^{4} + 27,793,973 \alpha^{3} - 6,084,932 \alpha^{2} \\ & + 495,906 \alpha + 900, \nonumber \\\sigma \theta \cdot \sigma^{2} \theta = & -2,171,688 \alpha^{14} + 67,084,221 \alpha^{13} - 934,645,093 \alpha^{12} + 7,750,575,584 \alpha^{11} \\ & - 42,508,235,392 \alpha^{10} + 162,029,379,062 \alpha^{9} - 438,947,076,273 \alpha^{8} \\ & + 849,307,812,685 \alpha^{7} - 1,162,572,370,875 \alpha^{6} + 1,098,352,512,421 \alpha^{5} \\& - 685,146,475,599 \alpha^{4} + 262,216,335,852 \alpha^{3} - 54,652,878,964 \alpha^{2} \\& + 5,143,605,707 \alpha - 112,645,567. \end{align*} $$
The three fields in Proposition 4.2 share the same Dedekind zeta function
 $$ \begin{align*} \zeta (s) = &\frac{1}{1^s} + \frac{4}{31^s}+ \frac{3}{32^s} + \frac{12}{61^s} + \frac{20}{125^s} + \frac{60}{311^s} + \frac{12}{373^s} + \frac{12}{433^s} \\[6pt] &+\frac{12}{557^s}+\frac{12}{619^s}+\frac{12}{683^s}+\frac{12}{743^s} + \frac{12}{929^s} + \frac{10}{961^s} + \frac{12}{991^s}+\frac{12}{992^s}+ \cdots. \end{align*} $$
$$ \begin{align*} \zeta (s) = &\frac{1}{1^s} + \frac{4}{31^s}+ \frac{3}{32^s} + \frac{12}{61^s} + \frac{20}{125^s} + \frac{60}{311^s} + \frac{12}{373^s} + \frac{12}{433^s} \\[6pt] &+\frac{12}{557^s}+\frac{12}{619^s}+\frac{12}{683^s}+\frac{12}{743^s} + \frac{12}{929^s} + \frac{10}{961^s} + \frac{12}{991^s}+\frac{12}{992^s}+ \cdots. \end{align*} $$
The referee pointed out that if we take the minimal polynomial of
![]() $2 \cos \left (\frac {2\pi }{31} \right )$
as f, then we can obtain elements with smaller coefficients.
$2 \cos \left (\frac {2\pi }{31} \right )$
as f, then we can obtain elements with smaller coefficients.
Acknowledgment
The author would like to thank the anonymous referee for his/her careful reading of the manuscript and many invaluable comments.