Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-26T19:57:00.883Z Has data issue: false hasContentIssue false
  • English
  • Français

Approximation and Interpolation by Entire Functions of Several Variables

Published online by Cambridge University Press:  20 November 2018

Maxim R. Burke
Maxim R. Burke*
Affiliation:
Department of Mathematics and Statistics, University of Prince Edward Island, Charlottetown, PE C1A 4P3 e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let $f\,:\,{{\mathbb{R}}^{n}}\,\to \,\mathbb{R}$ be 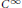${{C}^{\infty }}$ and let 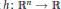$h\,:\,{{\mathbb{R}}^{n}}\,\to \,\mathbb{R}$ be positive and continuous. For any unbounded nondecreasing sequence 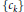$\{{{c}_{k}}\}$ of nonnegative real numbers and for any sequence without accumulation points 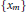$\{{{x}_{m}}\}$ in 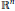${{\mathbb{R}}^{n}}$, there exists an entire function 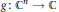$g\,:\,{{\mathbb{C}}^{n}}\,\to \,\mathbb{C}$ taking real values on 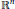${{\mathbb{R}}^{n}}$ such that

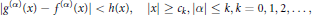$$\left| {{g}^{\left( \alpha \right)}}\left( x \right)-{{f}^{\left( \alpha \right)}}\left( x \right) \right|\text{ }<h\left( x \right),\left| x \right|\ge {{c}_{k}},\left| \alpha \right|\le k,k=0,1,2,...,$$

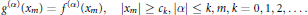$${{g}^{\left( \alpha \right)}}\left( {{x}_{m}} \right)\,=\,{{f}^{\left( \alpha \right)}}\left( {{x}_{m}} \right),\,\,\,\left| {{x}_{m}} \right|\,\ge \,{{c}_{k}},\,\left| \alpha \right|\,\le \,k,\,m,\,k\,=\,0,\,1,\,2,\,.\,.\,.\,.$$

This is a version for functions of several variables of the case 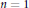$n\,=\,1$ due to $L$. Hoischen.

Keywords

32A15entire functioncomplex approximationinterpolationseveral complex variables
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 53 , Issue 1 , 01 March 2010 , pp. 11 - 22
Copyright
Copyright © Canadian Mathematical Society 2010

References

[Ca] Carleman, T., Sur un théorĕme de Weierstrass. Ark. Mat. Astronom. Fys. 20B(1927), 1–5.Google Scholar
[En] Engelking, R., General topology. Second edition, Sigma Series in Pure Mathematics 6, Heldermann Verlag, Berlin, 1989.Google Scholar
[FG] Frih, E. M. and Gauthier, P. M., Approximation of a function and its derivatives by entire functions of several variables. Canad. Math. Bull. 31(1988), no. 4, 495–499.Google Scholar
[GP] Gauthier, P. M. and Pouryayevali, M. R., Covering properties of most entire functions on Stein manifolds. Comput. Methods Funct. Theory 5(2005), no. 1, 223–235.Google Scholar
[GF] Grauert, H. and Fritsche, K., Several complex variables. Graduate Texts in Mathematics 38, Springer-Verlag, New York-Heidelberg, 1976.Google Scholar
[H1] Hoischen, L., Eine Verschärfung eines approximationssatzes von Carleman. J. Approximation Theory 9(1973), 272–277. doi:10.1016/0021-9045(73)90093-2Google Scholar
[H2] Hoischen, L., Approximation und Interpolation durch ganze Funktionen. J. Approximation Theory 15(1975), no. 2, 116–123. doi:10.1016/0021-9045(75)90121-5Google Scholar