Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Klep, Igor
2004.
The Noncommutative Graded Positivstellensatz.
Communications in Algebra,
Vol. 32,
Issue. 5,
p.
2029.
Lasserre, J.B.
2005.
SOS approximation of polynomials nonnegative on an algebraic set.
p.
5837.
Lasserre, Jean B.
2005.
Sum of Squares Approximation of Polynomials, Nonnegative on a Real Algebraic Set.
SIAM Journal on Optimization,
Vol. 16,
Issue. 2,
p.
610.
Ghasemi, Mehdi
Kuhlmann, Salma
and
Marshall, Murray
2014.
Application of Jacobiʼs representation theorem to locally multiplicatively convex topologicalR-algebras.
Journal of Functional Analysis,
Vol. 266,
Issue. 2,
p.
1041.
Ghasemi, Mehdi
Kuhlmann, Salma
and
Marshall, Murray
2016.
Moment problem in infinitely many variables.
Israel Journal of Mathematics,
Vol. 212,
Issue. 2,
p.
1012.
Blekherman, Grigoriy
Sinn, Rainer
and
Velasco, Mauricio
2017.
Do Sums of Squares Dream of Free Resolutions?.
SIAM Journal on Applied Algebra and Geometry,
Vol. 1,
Issue. 1,
p.
175.
Dinh, Trung Hoa
Ho, Minh Toan
and
Le, Cong Trinh
2021.
Positivstellensätze for polynomial matrices.
Positivity,
Vol. 25,
Issue. 4,
p.
1295.
Dressler, Mareike
and
Murray, Riley
2022.
Algebraic Perspectives on Signomial Optimization.
SIAM Journal on Applied Algebra and Geometry,
Vol. 6,
Issue. 4,
p.
650.
Infusino, Maria
Kuhlmann, Salma
Kuna, Tobias
and
Michalski, Patrick
2022.
Projective Limit Techniques for the Infinite Dimensional Moment Problem.
Integral Equations and Operator Theory,
Vol. 94,
Issue. 2,
Mai, Ngoc Hoang Anh
Lasserre, Jean-Bernard
and
Magron, Victor
2022.
Positivity certificates and polynomial optimization on non-compact semialgebraic sets.
Mathematical Programming,
Vol. 194,
Issue. 1-2,
p.
443.
Huang, Lei
Nie, Jiawang
and
Yuan, Ya-Xiang
2023.
Homogenization for polynomial optimization with unbounded sets.
Mathematical Programming,
Vol. 200,
Issue. 1,
p.
105.
Infusino, Maria
Kuhlmann, Salma
Kuna, Tobias
and
Michalski, Patrick
2023.
An Intrinsic Characterization of Moment Functionals in the Compact Case.
International Mathematics Research Notices,
Vol. 2023,
Issue. 3,
p.
2281.
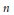 $n$-space. The emphasis is on the non-compact case and on quadratic module representations as opposed to quadratic preordering presentations. The paper clarifies the relationship between known results on the algebraic side and on the functional-analytic side and extends these results in a variety of ways.
$n$-space. The emphasis is on the non-compact case and on quadratic module representations as opposed to quadratic preordering presentations. The paper clarifies the relationship between known results on the algebraic side and on the functional-analytic side and extends these results in a variety of ways.

