Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Shen, J.H.
and
Stavroulakis, I.P.
2000.
Oscillatory and Nonoscillatory Delay Equations with Piecewise Constant Argument.
Journal of Mathematical Analysis and Applications,
Vol. 248,
Issue. 2,
p.
385.
Shen, Jianhua
and
Tang, Xianhua
2004.
New nonoscillation criteria for delay differential equations.
Journal of Mathematical Analysis and Applications,
Vol. 290,
Issue. 1,
p.
1.
Zhao, Aimin
Tang, Xianhua
and
Yan, Jurang
2004.
Oscillation of first-order delay differential equations.
The ANZIAM Journal,
Vol. 45,
Issue. 4,
p.
593.
Kikina, L. K.
Stavroulakis, I. P.
and
Berezansky, Leonid
2010.
Oscillation Criteria for Second‐Order Delay, Difference, and Functional Equations.
International Journal of Differential Equations,
Vol. 2010,
Issue. 1,
Stavroulakis, Ioannis P
2014.
A survey on the oscillation of differential equations with several deviating arguments.
Journal of Inequalities and Applications,
Vol. 2014,
Issue. 1,
Stavroulakis, I.P.
2014.
Oscillation criteria for delay and difference equations with non-monotone arguments.
Applied Mathematics and Computation,
Vol. 226,
Issue. ,
p.
661.
El-Morshedy, Hassan A.
and
Attia, Emad R.
2016.
New oscillation criterion for delay differential equations with non-monotone arguments.
Applied Mathematics Letters,
Vol. 54,
Issue. ,
p.
54.
Moremedi, G. M.
and
Stavroulakis, I. P.
2018.
Differential and Difference Equations with Applications.
Vol. 230,
Issue. ,
p.
441.
Dorociaková, Božena
Chupáč, Radoslav
and
Olach, Rudolf
2018.
Notes on oscillation of linear delay differential equations.
Advances in Difference Equations,
Vol. 2018,
Issue. 1,
Stavroulakis, Ioannis P.
and
Xenos, Michail A.
2020.
Computational Mathematics and Variational Analysis.
Vol. 159,
Issue. ,
p.
465.
Attia, Emad R.
El-Morshedy, Hassan A.
and
Stavroulakis, Ioannis P.
2020.
Oscillation Criteria for First Order Differential Equations with Non-Monotone Delays.
Symmetry,
Vol. 12,
Issue. 5,
p.
718.
KILIÇ, Nurten
2021.
Oscillation Test for Linear Delay Differential Equation with Nonmonotone Argument.
Turkish Journal of Mathematics and Computer Science,
Vol. 13,
Issue. 2,
p.
310.
KILIÇ, Nurten
and
ÖCALAN, Özkan
2021.
Oscillation criteria for first-order dynamic equations with nonmonotone delays.
Hacettepe Journal of Mathematics and Statistics,
Vol. 50,
Issue. 2,
p.
318.
Zhuang, Ziwei
Wang, Qiru
and
Wu, Hongwu
2021.
A new oscillation criterion for first-order delay differential equations by iteration.
Applied Mathematics and Computation,
Vol. 390,
Issue. ,
p.
125632.
Zhuang, Ziwei
Wang, Qiru
and
Wu, Hongwu
2021.
A partly sharp oscillation criterion for first-order delay differential equations.
Applied Mathematics and Computation,
Vol. 409,
Issue. ,
p.
126422.
Pituk, Mihály
Stavroulakis, Ioannis P.
and
Stavroulakis, John Ioannis
2023.
Explicit values of the oscillation bounds for linear delay differential equations with monotone argument.
Communications in Contemporary Mathematics,
Vol. 25,
Issue. 03,
Stavroulakis, Ioannis P.
2024.
A Survey on the Oscillation of First-Order Retarded Differential Equations.
Axioms,
Vol. 13,
Issue. 6,
p.
407.
 ${x}'\,(t)\,+\,p(t)x\,(t\,-\,\text{ }\!\!\tau\!\!\text{ (t)})\,=\,0$, where
${x}'\,(t)\,+\,p(t)x\,(t\,-\,\text{ }\!\!\tau\!\!\text{ (t)})\,=\,0$, where 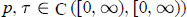 $p,\,\text{ }\!\!\tau\!\!\text{ }\,\in \,\text{C}\,\text{( }\!\ $T$ defined by
$T$ defined by 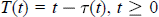 $T(t)\,=\,t-\,\text{ }\!\!\tau\!\!\text{ }\,\text{(t),}\,\text{t}\ge \,\text{0}$ is increasing and such that
$T(t)\,=\,t-\,\text{ }\!\!\tau\!\!\text{ }\,\text{(t),}\,\text{t}\ge \,\text{0}$ is increasing and such that 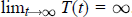 ${{\lim }_{t\to \infty }}\,T(t)\,=\,\infty $. This criterion concerns the case where
${{\lim }_{t\to \infty }}\,T(t)\,=\,\infty $. This criterion concerns the case where 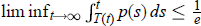 $\lim \,{{\inf }_{t\to \infty }}\int _{T(t)}^{t}p(s)ds\le \frac{1}{e}$.
$\lim \,{{\inf }_{t\to \infty }}\int _{T(t)}^{t}p(s)ds\le \frac{1}{e}$.

