Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-27T12:31:13.707Z Has data issue: false hasContentIssue false
  • English
  • Français

An Optimal Transport View of Schrödinger's Equation

Published online by Cambridge University Press:  20 November 2018

Max-K. von Renesse
Max-K. von Renesse*
Affiliation:
Technische Universität Berline-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

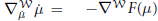We show that the Schrödinger equation is a lift of Newton's third law of motion $\nabla _{{\dot{\mu }}}^{\mathcal{W}}\,\dot{\mu }\,=\,-{{\nabla }^{\mathcal{W}}}\,F\left( \mu \right)$ on the space of probability measures, where derivatives are taken with respect to the Wasserstein Riemannian metric. Here the potential 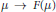$\mu \,\to \,F\left( \mu \right)$ is the sum of the total classical potential energy 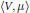$\left\langle V,\,\mu \right\rangle $ of the extended system and its Fisher information 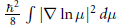$\frac{{{\hbar }^{2}}}{8}\,{{\int{\left| \nabla \,\text{1n}\,\mu \right|}}^{2}}\,d\mu $. The precise relation is established via a well-known (Madelung) transform which is shown to be a symplectic submersion of the standard symplectic structure of complex valued functions into the canonical symplectic space over the Wasserstein space. All computations are conducted in the framework of Otto's formal Riemannian calculus for optimal transportation of probability measures.

Keywords

81C2582C7037K05Schrödinger equationoptimal transportNewton's lawsymplectic submersion
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 55 , Issue 4 , 01 December 2012 , pp. 858 - 869
Copyright
Copyright © Canadian Mathematical Society 2012

References

[1] Abraham, R. and Marsden, J. E., Foundations of Mechanics. Second edition. Benjamin/Cummings Publishing, Reading, MA, 1978.Google Scholar
[2] Ambrosio, L. and Gangbo, W., Hamiltonian ODEs in the Wasserstein space of probability measures. Comm. Pure Appl. Math. 61(2008), no. 1, 18–53. http://dx.doi.org/10.1002/cpa.20188 Google Scholar
[3] Ambrosio, L., Gigli, N., and Savaré, G., Gradient flows in metric spaces and in the space of probability measures. Lectures in Mathematics ETH ZÜrich. Birkhäuser Verlag, Basel, 2005.Google Scholar
[4] Benamou, J.-D. and Brenier, Y., A computational fluid mechanics solution to the Monge-Kantorovich mass transfer problem. Numer. Math. 84(2000), no. 3, 375–393. http://dx.doi.org/10.1007/s002110050002 Google Scholar
[5] Bohm, D.. A suggested interpretation of the quantum theory in terms of “hidden” variables. I, II. Physical Rev. 85(1952), 166–193. http://dx.doi.org/10.1103/PhysRev.85.166 Google Scholar
[6] Cordero-Erausquin, D., McCann, R. J., and Schmuckenschläger, M., A Riemannian interpolation inequality à la Borell, Brascamp and Lieb. Invent. Math. 146(2001), no. 2, 219–257. http://dx.doi.org/10.1007/s002220100160 Google Scholar
[7] Gangbo, W., Nguyen, T., and Tudorascu, A., Hamilton-Jacobi equations in the Wasserstein space. Methods Appl. Anal. 15(2008), no. 2, 155–183.Google Scholar
[8] Gianazza, U., Savare, G., and Toscani, G., The Wasserstein gradient flow of the Fisher information and the quantum drift-diffusion equation. Arch. Rat. Mech. Anal. To appear. http://dx.doi.org/10.1007/s00205-008-0186-5 Google Scholar
[9] Hall, M. J. W. and Reginatto, M., Schrödinger equation from an exact uncertainty principle. J. Phys. A 35(2002), no. 14, 3289–3303. http://dx.doi.org/10.1088/0305-4470/35/14/310 Google Scholar
[10] Lafferty, J. D., The density manifold and configuration space quantization. Trans. Amer. Math. Soc. 305(1988), no. 2, 699–741. http://dx.doi.org/10.1090/S0002-9947-1988-0924776-9 Google Scholar
[11] Lott, J., Some geometric calculations on Wasserstein space. Comm. Math. Phys. 277(2008), no. 2, 423–437. http://dx.doi.org/10.1007/s00220-007-0367-3 Google Scholar
[12] Madelung, E., Quantentheorie in hydrodynamischer Form. Z. Phys. 40(1926), 322–326.Google Scholar
[13] McCann, R. J., Polar factorization of maps on Riemannian manifolds. Geom. Funct. Anal. 11(2001), no. 3, 589–608. http://dx.doi.org/10.1007/PL00001679 Google Scholar
[14] Nelson, E., Quantum fluctuations. Princeton Series in Physics. Princeton University Press, Princeton, NJ, 1985.Google Scholar
[15] Otto, F., The geometry of dissipative evolution equations: the porous medium equation. Comm. Partial Differential Equations 26(2001), no. 1-2, 101–174. http://dx.doi.org/10.1081/PDE-100002243 Google Scholar
[16] Otto, F. and Villani, C., Generalization of an inequality by Talagrand and links with the logarithmic Sobolev inequality. J. Funct. Anal. 173(2000), no. 2, 361–400. http://dx.doi.org/10.1006/jfan.1999.3557 Google Scholar
[17] Villani, C., Topics in optimal transportation. Graduate Studies in Mathematics 58. American Mathematical Society, Providence, RI, 2003.Google Scholar
[18] Völlinger, S., Geometry of the Schrödinger equation and stochastic mass transportation. J. Math. Phys. 46(2005), no. 8, 082105. http://dx.doi.org/10.1063/1.1998835 Google Scholar
[19] von Renesse, M.-K. and Sturm, K.-T., Transport inequalities, gradient estimates, entropy, and Ricci curvature. Comm. Pure Appl.Math. 58(2005), no. 7, 923–940. http://dx.doi.org/10.1002/cpa.20060 Google Scholar
[20] von Renesse, M.-K. and Sturm, K.-T., Entropic measure and Wasserstein diffusion. Ann. Probab. 37(2009), no. 3, 1114–1191. http://dx.doi.org/10.1214/08-AOP430 Google Scholar