Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-28T04:02:22.546Z Has data issue: false hasContentIssue false
  • English
  • Français

An Elementary Probabilistic Computation of the Poisson Kernel for the n = 2 and 3 Euclidean Ball

Published online by Cambridge University Press:  20 November 2018

Jacques Vauthier
Jacques Vauthier*
Affiliation:
Department of Mathematics, University of Toronto, Toronto, Canada, M5S1A1
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Direct and elementary derivation of the classical Poisson kernel for the ball in n = 2 or n = 3 dimensions starting with the usual expression 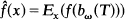involving the brownian motion bω, the stopping time T on the boundary, and Ex the conditional expectation on paths starting at x.

Keywords

kw60J4560J65Poisson kernelsBrownian motionMartingale
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 27 , Issue 2 , 01 June 1984 , pp. 241 - 246
Copyright
Copyright © Canadian Mathematical Society 1984

References

1. Gaveau, B. and Vauthier, J., Intégrales oscillantes stochastiques: L’équation de Pauli, Journal of Functional Analysis 44 (1981), pp. 388–400.Google Scholar
2. Levy, P., Le mouvement Brownien, Gauthier-Villars, Paris (1954).Google Scholar
3. MacKean, H. P., Stochastic integrals, Academic Press (1969).Google Scholar
4. Greiner, P., Special harmonies on the Heisenberg group, Canadian Mathematical Bulletin Vol. 23 (1980), pp. 383–393.Google Scholar