Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kucharzewski, M.
1970.
Einige Bemerkungen über eine Differenzenfunktionalgleichung.
Aequationes Mathematicae,
Vol. 5,
Issue. 2-3,
p.
285.
Haruki, Hiroshi
1970.
On the Functional Equationf(x+t,y)+f(x−t,y)=f(x,y+t)+f(x, y−t).
Aequationes Mathematicae,
Vol. 5,
Issue. 1,
p.
118.
von Leissner, W.
1971.
Achte Internationale Tagung über Funktionalgleichungen in Oberwolfach vom 2.–8. August 1970.
aequationes mathematicae,
Vol. 6,
Issue. 1,
p.
90.
McKiernan, M. A.
1972.
The general solution of some finite difference equations analogous to the wave equation.
Aequationes Mathematicae,
Vol. 8,
Issue. 3,
p.
263.
Flemming, D. P.
1972.
Generalizations of the Wave Equation which Allow Weak and Strong Discontinuities.
SIAM Journal on Applied Mathematics,
Vol. 23,
Issue. 2,
p.
221.
Fenyö, I.
1972.
Remark on a paper of J. A. Baker.
Aequationes Mathematicae,
Vol. 8,
Issue. 1-2,
p.
103.
Girod, Donald
1973.
On the Functional Equation $$\Delta _{T_{1y} } \Delta _{T_{2y} } f = 0$$.
Aequationes Mathematicae,
Vol. 9,
Issue. 2-3,
p.
157.
Zalcman, Lawrence
1973.
Mean values and differential equations.
Israel Journal of Mathematics,
Vol. 14,
Issue. 4,
p.
339.
Światak, Halina
1976.
The regularity of the locally integrable and continuous solutions of nonlinear functional equations.
Transactions of the American Mathematical Society,
Vol. 221,
Issue. 1,
p.
97.
Haruki, Shigeru
1980.
Note on the equation $$\left( {\mathop {\Delta ^2 }\limits_{x,t} - \mathop {\Delta ^2 }\limits_{y,t} } \right)f = 0$$.
Aequationes Mathematicae,
Vol. 21,
Issue. 1,
p.
49.
Laird, P. G.
and
Mills, J.
1983.
On systems of linear functional equations.
Aequationes Mathematicae,
Vol. 26,
Issue. 1,
p.
64.
Haruki, Shigeru
1985.
A nonsymmetric partial difference functional equation analogous to the wave equation.
Proceedings of the Japan Academy, Series A, Mathematical Sciences,
Vol. 61,
Issue. 9,
Fenyö, István
1987.
On the hyperbolic linear functional equations.
Aequationes Mathematicae,
Vol. 32,
Issue. 1,
p.
252.
Haruki, Shigeru
1988.
On the general solution of a nonsymmetric partial difference functional equation analogous to the wave equation.
Aequationes Mathematicae,
Vol. 36,
Issue. 1,
p.
20.
Chlebík, Miroslav
and
Král, Josef
1994.
Removability of the wave singularities in the plane.
Aequationes Mathematicae,
Vol. 47,
Issue. 2-3,
p.
123.
Chung, Jukang
Kannappan, Palaniappan
and
Sahoo, Prasanna K.
1997.
On trigonometric functional equations of rectangular type.
Aequationes Mathematicae,
Vol. 53,
Issue. 1-2,
p.
36.
Fenyö, I.
2010.
Functional Equations and Inequalities.
p.
43.


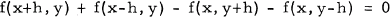
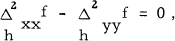
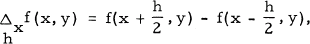 etc., (i. e. symmetric h differences), and that (1) has an interesting geometric interpretation. The continuous solutions of (1) were found by Sakovič [5].
etc., (i. e. symmetric h differences), and that (1) has an interesting geometric interpretation. The continuous solutions of (1) were found by Sakovič [5].