Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-26T21:25:42.589Z Has data issue: false hasContentIssue false
  • English
  • Français

Alternating Chebyshev Approximation with A Non-Continuous Weight Function

Published online by Cambridge University Press:  20 November 2018

Charles B. Dunham
Charles B. Dunham*
Affiliation:
Computer Science Department, University of Western Ontario, London, Ontario, Canada
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let [α, β] be a closed interval and C[α, β] be the space of continuous functions on [α, β], For g a function on [α, β] define

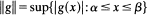
Let s be a non-negative function on [α, β]. Let F be an approximating function with parameter space P such that F(A, .)∊ C[α, β] for all A∊P. The Chebyshev problem with weight s is given f ∊ C[α, β], to find a parameter A* ∊ P to minimize e(A) = ||s * (f - F(A, .))|| over A∊P. Such a parameter A* is called best and F(A*,.) is called a best approximation to f.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 19 , Issue 2 , 01 June 1976 , pp. 155 - 157
Copyright
Copyright © Canadian Mathematical Society 1976

References

1. Dunham, C. B.. Chebyshev approximation with respect to a weight function, J. Approximation Theory 2 (1969), 223–232.CrossRefGoogle Scholar
2. Rice, J. R., The Approximation of Functions, Volume 2, Addison-Wesley, Reading, Mass., 1969.Google Scholar