No CrossRef data available.
Article contents
Algebraic Values of Entire Functions with Extremal Growth Orders: An Extension of a Theorem of Boxall and Jones
Published online by Cambridge University Press: 15 October 2019
Abstract
Given an entire function 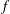 $f$ of finite order
$f$ of finite order 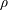 $\unicode[STIX]{x1D70C}$ and positive lower order
$\unicode[STIX]{x1D70C}$ and positive lower order 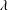 $\unicode[STIX]{x1D706}$, Boxall and Jones proved a bound of the form
$\unicode[STIX]{x1D706}$, Boxall and Jones proved a bound of the form 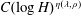 $C(\log H)^{\unicode[STIX]{x1D702}(\unicode[STIX]{x1D706},\unicode[STIX]{x1D70C})}$ for the density of algebraic points of bounded degree and height at most
$C(\log H)^{\unicode[STIX]{x1D702}(\unicode[STIX]{x1D706},\unicode[STIX]{x1D70C})}$ for the density of algebraic points of bounded degree and height at most 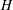 $H$ on the restrictions to compact sets of the graph of
$H$ on the restrictions to compact sets of the graph of  $f$. The constant
$f$. The constant 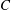 $C$ and exponent
$C$ and exponent 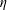 $\unicode[STIX]{x1D702}$ are effectively computable from certain data associated with the function. In this followup note, using different measures of the growth of entire functions, we obtain similar bounds for other classes of functions to which the original theorem does not apply.
$\unicode[STIX]{x1D702}$ are effectively computable from certain data associated with the function. In this followup note, using different measures of the growth of entire functions, we obtain similar bounds for other classes of functions to which the original theorem does not apply.
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2019
Footnotes
This article was completed under the Fields-AIMS-Perimeter postdoctoral fellowship, provided by the Fields Institute for Research in Mathematical Sciences.



