Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-29T11:24:28.906Z Has data issue: false hasContentIssue false
  • English
  • Français

Abstract Plancherel (Trace) Formulas over Homogeneous Spaces of Compact Groups

Published online by Cambridge University Press:  20 November 2018

Arash Ghaani Farashahi
Arash Ghaani Farashahi*
Affiliation:
Numerical Harmonic Analysis Group (NuHAG), Faculty of Mathematics, University of Vienna, Oskar- Morgenstern-Platz 1 A-1090 Wien, Vienna, Austria e-mail: [email protected] [email protected] e-mail: [email protected] [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

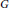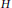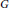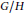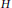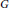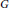This paper introduces a unified operator theory approach to the abstract Plancherel (trace) formulas over homogeneous spaces of compact groups. Let $G$ be a compact group and let $H$ be a closed subgroup of $G$. Let ${G}/{H}\;$ be the left coset space of $H$ in $G$ and let $\mu$ be the normalized $G$-invariant measure on 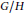${G}/{H}\;$ associated with Weil’s formula. Then we present a generalized abstract notion of Plancherel (trace) formula for the Hilbert space 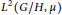${{L}^{2}}\left( {G}/{H,\,\mu }\; \right)$.

Keywords

20G0543A8543A3243A40compact grouphomogeneous spacedual spacePlancherel (trace) formula
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 60 , Issue 1 , 01 March 2017 , pp. 111 - 121
Copyright
Copyright © Canadian Mathematical Society 2017

References

[1] Folland, G. B., A course in abstract harmonie analysis. CRC Press, Boca Raton, FL, 1995.Google Scholar
[2] Forrest, B., Fourier analysis on coset spaces. Rocky Mount. J. Math. 28(1998), no. 1,173-190. http://dx.doi.Org/1 0.121 6/rmjm/11 81071 828 Google Scholar
[3] Führ, H., Abstract harmonic analysis of continuous wavelet transforms. Lecture Notes in Mathematics, 1863, Springer-Verlag, Berlin, 2005.Google Scholar
[4] Ghaani Farashahi, A., Abstract harmonic analysis of wave packet transforms over locally compact abelian groups. Banach J. Math. Anal., to appear.Google Scholar
[5] Ghaani Farashahi, A., Abstract harmonic analysis of relative convolutions over canonical homogeneous spaces of semidirect product groups. J. Aust. Math. Soc, to appear. http://dx.doi.Org/10.1017/S1446788715000798 Google Scholar
[6] Ghaani Farashahi, A., Abstract relative Fourier transforms over canonical homogeneous spaces of semi-direct product groups with Abelian normal factor. J. Korean Math. Soc. (2016) http://dx.doi.Org/10.4134/JKMS.j150610 Google Scholar
[7] Ghaani Farashahi, A., A unified group theoretical methodfor the partial Fourier analysis on semi-direct product of locally compact groups. Results Math. 67(2015), no. 1-2, 235–251. http://dx.doi.Org/10.1007/s00025-014-0407-1 Google Scholar
[8] Ghaani Farashahi, A., Convolution and involution on function spaces of homogeneous spaces. Bull. Malays. Math. Sci. Soc. (2) 36(2013), no. 4,1109-1122.Google Scholar
[9] Hewitt, E. and Ross, K. A., Abstract harmonic analysis. Vol. 1, Springer, Berlin, 1963.Google Scholar
[10] Hewitt, E. and Ross, K. A., Abstract harmonic analysis. Structure and analysis for compact groups. Analysis on locally compact Abelian groups. Vol. 2, Die Grundlehren der mathematischen Wissenschaften, 152, Springer-Verlag, New York-Berlin, 1970.Google Scholar
[11] Kisil, V., Calculus of operators: covariant transform and relative convolutions. Banach J. Math. Anal. 8(2014), no. 2, 156–184. http://dx.doi.Org/10.1 5352/bjma/1396640061 Google Scholar
[12] Kisil, V., Geometry ofMôbius transformations. Elliptic, parabolic and hyperbolic actions of SL2(R). Imperial College Press, London, 2012. http://dx.doi.Org/10.1142/p835 Google Scholar
[13] Kisil, V., Relative convolutions. I. Properties and applications. Adv. Math. 147(1999), no. 1, 35–73. http://dx.doi.Org/1 0.1006/aima.1 999.1 833 Google Scholar
[14] Lipsman, R. L., The Plancherel formula for homogeneous spaces with exponential spectrum. J. Reine Angew. Math. 500(1998), 49–63. http://dx.doi.Org/10.1515/crll.1 998.069 Google Scholar
[15] Lipsman, R. L., A unified approach to concrete Plancherel theory of homogeneous spaces. Manuscripta Math. 94(1997), no. 2, 133–149. http://dx.doi.Org/10.1007/BF02677843 Google Scholar
[16] Lipsman, R. L., The Penney-Fujiwara Plancherel formula for Gelfand pairs. Rocky Mountain J. Math. 26(1996), no. 2, 655–677. http://dx.doi.Org/1 0.121 6/rmjm/11 81072078 Google Scholar
[17] Lipsman, R. L., The Plancherel formula for homogeneous spaces with polynomial spectrum. Pacific J. Math. 159(1993), no. 2, 351–377. http://dx.doi.Org/10.2140/pjm.1993.159.351 Google Scholar
[18] Lipsman, R. L., Non-Abelian Fourier analysis. Bull. Sci. Math. (2) 981974), no. 4, 209–233.Google Scholar
[19] Murphy, G. J., C*-algebras and operator theory. Academic Press, Boston, MA, 1990.Google Scholar
[20] Reiter, H. and Stegeman, J. D., Classical harmonic analysis and locally compact groups. Second éd., London Mathematical Society Monographs, 22, Oxford University Press, New York, 2000.Google Scholar
[21] Segal, I. E., An extension of Plancherel's formula to separable unimodular groups. Ann. of Math. 52(1950), 272–292. http://dx.doi.Org/! 0.2307/1 969470 Google Scholar