No CrossRef data available.
Article contents
The virtually generating graph of a profinite group
Published online by Cambridge University Press: 15 October 2020
Abstract
We consider the graph
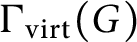 $\Gamma _{\text {virt}}(G)$
whose vertices are the elements of a finitely generated profinite group G and where two vertices x and y are adjacent if and only if they topologically generate an open subgroup of G. We investigate the connectivity of the graph
$\Gamma _{\text {virt}}(G)$
whose vertices are the elements of a finitely generated profinite group G and where two vertices x and y are adjacent if and only if they topologically generate an open subgroup of G. We investigate the connectivity of the graph
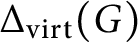 $\Delta _{\text {virt}}(G)$
obtained from
$\Delta _{\text {virt}}(G)$
obtained from
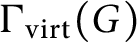 $\Gamma _{\text {virt}}(G)$
by removing its isolated vertices. In particular, we prove that for every positive integer t, there exists a finitely generated prosoluble group G with the property that
$\Gamma _{\text {virt}}(G)$
by removing its isolated vertices. In particular, we prove that for every positive integer t, there exists a finitely generated prosoluble group G with the property that
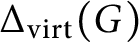 $\Delta _{\operatorname {\mathrm {virt}}}(G)$
has precisely t connected components. Moreover, we study the graph
$\Delta _{\operatorname {\mathrm {virt}}}(G)$
has precisely t connected components. Moreover, we study the graph
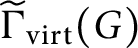 $\widetilde \Gamma _{\operatorname {\mathrm {virt}}}(G)$
, whose vertices are again the elements of G and where two vertices are adjacent if and only if there exists a minimal generating set of G containing them. In this case, we prove that the subgraph
$\widetilde \Gamma _{\operatorname {\mathrm {virt}}}(G)$
, whose vertices are again the elements of G and where two vertices are adjacent if and only if there exists a minimal generating set of G containing them. In this case, we prove that the subgraph
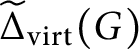 $\widetilde \Delta _{\operatorname {\mathrm {virt}}}(G)$
obtained removing the isolated vertices is connected and has diameter at most 3.
$\widetilde \Delta _{\operatorname {\mathrm {virt}}}(G)$
obtained removing the isolated vertices is connected and has diameter at most 3.
MSC classification
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2020



