On the sign changes of Dirichlet coefficients of triple product L-functions

Abstract

Let f and g be two distinct normalized primitive holomorphic cusp forms of even integral weight 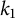$k_{1}$ and 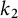$k_{2}$ for the full modular group 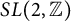$SL(2,\mathbb {Z})$, respectively. Suppose that 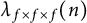$\lambda _{f\times f\times f}(n)$ and 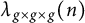$\lambda _{g\times g\times g}(n)$ are the n-th Dirichlet coefficient of the triple product L-functions 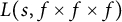$L(s,f\times f\times f)$ and 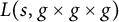$L(s,g\times g\times g)$. In this paper, we consider the sign changes of the sequence 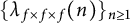$\{\lambda _{f\times f\times f}(n)\}_{n\geq 1}$ and 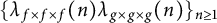$\{\lambda _{f\times f\times f}(n)\lambda _{g\times g\times g}(n)\}_{n\geq 1}$ in short intervals and establish quantitative results for the number of sign changes for 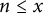$n \leq x$, which improve the previous results.