No CrossRef data available.
Article contents
On the greatest common divisor of n and the nth Fibonacci number, II
Published online by Cambridge University Press: 06 October 2022
Abstract
Let
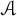 $\mathcal {A}$
be the set of all integers of the form
$\mathcal {A}$
be the set of all integers of the form
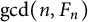 $\gcd (n, F_n)$
, where n is a positive integer and
$\gcd (n, F_n)$
, where n is a positive integer and
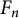 $F_n$
denotes the nth Fibonacci number. Leonetti and Sanna proved that
$F_n$
denotes the nth Fibonacci number. Leonetti and Sanna proved that
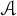 $\mathcal {A}$
has natural density equal to zero, and asked for a more precise upper bound. We prove that
$\mathcal {A}$
has natural density equal to zero, and asked for a more precise upper bound. We prove that
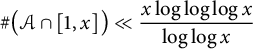 $$ \begin{align*} \#\big(\mathcal{A} \cap [1, x]\big) \ll \frac{x \log \log \log x}{\log \log x} \end{align*} $$
$$ \begin{align*} \#\big(\mathcal{A} \cap [1, x]\big) \ll \frac{x \log \log \log x}{\log \log x} \end{align*} $$
- Type
- Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of The Canadian Mathematical Society



