Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-25T01:49:45.307Z Has data issue: false hasContentIssue false
  • English
  • Français

On cohesive almost zero-dimensional spaces

Part of: Special properties Fairly general properties Peculiar spaces

Published online by Cambridge University Press:  15 July 2020

Jan J. Dijkstra  and
David S. Lipham
Jan J. Dijkstra
Affiliation:
PO Box 1180, Crested Butte, CO81224, USA e-mail: [email protected]
David S. Lipham*
Affiliation:
Department of Mathematics, Auburn University at Montgomery, Montgomery, AL36117, USA e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate C-sets in almost zero-dimensional spaces, showing that closed 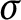$\sigma $ C-sets are C-sets. As corollaries, we prove that every rim-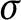 $\sigma $ -compact almost zero-dimensional space is zero-dimensional and that each cohesive almost zero-dimensional space is nowhere rational. To show that these results are sharp, we construct a rim-discrete connected set with an explosion point. We also show that every cohesive almost zero-dimensional subspace of 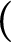$($ Cantor set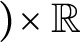 $)\!\times \mathbb R$ is nowhere dense.

Keywords

Almost zero-dimensionalcohesiverationalLelek fanexplosion pointErdős space

MSC classification

Primary: 54F45: Dimension theory 54F50: Spaces of dimension $leq 1$; curves, dendrites 54D35: Extensions of spaces (compactifications, supercompactifications, completions, etc.) 54G20: Counterexamples
Type
Article
Information
Canadian Mathematical Bulletin , Volume 64 , Issue 2 , June 2021 , pp. 429 - 441
Check for updates
Copyright
© Canadian Mathematical Society 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abry, M., Dijkstra, J. J., and van Mill, J., On one-point connectifications . Topol. Appl. 154(2007), 725–733. https://doi.org/10.1016/j.topol.2006.09.004 CrossRefGoogle Scholar
Alhabib, N. and Rempe-Gillen, L., Escaping endpoints explode . Comput. Methods Funct. Theory 17(2017), 65–100. https://doi.org/10.1007/s40315-016-0169-8 CrossRefGoogle Scholar
Banakh, T., Answer to math overflow question: “Scattered separators of Erdős space”. MathOverflow, 2019. https://mathoverflow.net/questions/324121.Google Scholar
Brouwer, L. E. J., Lebesgueshes mass und analysis situs . Math. Ann. 79(1918), 212–222. https://doi.org/10.1007/BF01458204 CrossRefGoogle Scholar
Bula, W. D. and Oversteegen, L. G., A characterization of smooth Cantor bouquets . Proc. Am. Math. Soc. 108(1990), 529–534. https://doi.org/10.2307/2048305 CrossRefGoogle Scholar
Charatonik, W. J., The Lelek fan is unique . Houston J. Math. 15(1989), 27–34.Google Scholar
Cook, H., Ingram, W. T., and Lelek, A., A list of problems known as Houston problem book . In: Continua with the Houston Problem Book Lecture Notes in Pure and Appl. Math., 170, Dekker, New York, NY, 1995, pp 365–398.Google Scholar
Dijkstra, J. J., On homeomorphism groups of Menger continua . Trans. Am. Math. Soc. 357(2005), 2665–2679. https://doi.org/10.1090/S0002-9947-05-03863-8 CrossRefGoogle Scholar
Dijkstra, J. J., A criterion for Erdős spaces . Proc. Edinb. Math. Soc. 48(2005), 595–601. https://doi.org/10.1017/S0013091504000823 CrossRefGoogle Scholar
Dijkstra, J. J., A homogeneous space that is one-dimensional but not cohesive . Houston J. Math. 32(2006), 1093–1099.Google Scholar
Dijkstra, J. J., Characterizing stable complete Erdős space . Israel J. Math. 186(2011), 477–507. https://doi.org/10.1007/s11856-011-0149-7 CrossRefGoogle Scholar
Dijkstra, J. J. and van Mill, J., Erdős space and homeomorphism groups of manifolds . Mem. Am. Math. Soc. 208(2010), no. 979, 1–62. https://doi.org/10.1090/S0065-9266-10-00579-X Google Scholar
Dijkstra, J. J. and van Mill, J., Negligible sets in Erdős spaces . Topol. Appl. 159(2012), 2947–2950. https://doi.org/10.1016/j.topol.2012.05.006 CrossRefGoogle Scholar
Dovgoshey, O., Martio, O., Ryazanov, V., and Vuorinen, M., The cantor function . Exp. Math. 24(2006), 1–37. https://doi.org/10.1016/j.exmath.2005.05.002 CrossRefGoogle Scholar
Duda, R., On biconnected sets with dispersion points . Rozprawy Mat. 37(1964), 1–59.Google Scholar
Engelking, R., Dimension theory . In: North-Holland mathematical library, Vol. 19, North-Holland, Amsterdam, Netherlands, 1978.Google Scholar
Engelking, R., General topology . In: Sigma series in pure mathematics, Vol. 6, 2nd ed., Heldermann, Berlin, Germany, 1989.Google Scholar
Erdős, P., The dimension of the rational points in Hilbert space . Ann. Math. 41(1940), 734–736. https://doi.org/10.2307/1968851 CrossRefGoogle Scholar
Iliadis, S. D., A note on compactifications of rim-scattered spaces . Topol. Proc. 5th Int. Meet., Lecce/Italy 1990, Suppl. Rend. Circ. Mat. Palermo, II. Ser. 29(1992) 425–433.Google Scholar
Iliadis, S. D. and Tymchatyn, E. D., Compactifications with minimum rim-types of rational spaces . Houston J. Math. 17(1991) 311–323.Google Scholar
Jech, T., Set theory. The 3rd millennium ed., revised and expanded, Springer Monographs in Mathematics, Springer-Verlag, Berlin, Germany, 2003.Google Scholar
Jones, F. B., Connected and disconnected plane sets and the functional equation $f(x)+f(y)= f\left(x+y\right)$ . Bull. Am. Math. Soc. 48(1942), 115–120. https://doi.org/10.1090/S0002-9904-1942-07615-4 CrossRefGoogle Scholar
Kawamura, K., Oversteegen, L. G., and Tymchatyn, E. D., On homogeneous totally disconnected $1$ -dimensional spaces . Fund. Math. 150(1996), 97–112.Google Scholar
Kuratowski, K., Topology. Vol. II, Academic Press, New York, NY, 1968.Google Scholar
Kuratowski, K. and Ulam, S., Quelques propriétés topologiques du produit combinatiore . Fund. Math. 19(1932), 247–251.CrossRefGoogle Scholar
Lelek, A., Ensembles $\sigma$ -connexes et le théorème de Gehman . Fund. Math. 47(1959), 265–276. https://doi.org/10.4064/fm-47-3-265-276 CrossRefGoogle Scholar
Lelek, A., On plane dendroids and their end points in the classical sense . Fund. Math. 49(1960/1961), 301–319. https://doi.org/10.4064/fm-49-3-301-319 CrossRefGoogle Scholar
Lelek, A., On the topology of curves II . Fund. Math. 70(1971), 131–138. https://doi.org/10.4064/fm-70-2-131-138 CrossRefGoogle Scholar
Lipham, D. S., Widely-connected sets in the bucket-handle continuum . Fund. Math. 240(2018), 161–174. https://doi.org/10.4064/fm378-3-2017 CrossRefGoogle Scholar
Lipham, D. S., Dispersion points and rational curves . Proc. Am. Math. Soc. 148(2020), 2671–2682. https://doi.org/10.1909/proc/14920 CrossRefGoogle Scholar
Lipham, D. S., A note on the topology of escaping endpoints . Ergodic Theory Dyn. Syst. (2020), to appear.Google Scholar
Nishiura, T. and Tymchatyn, E. D., Hereditarily locally connected spaces . Houston J. Math. 2(1976), 581–599.Google Scholar
Oversteegen, L. G. and Tymchatyn, E. D., On the dimension of certain totally disconnected spaces . Proc. Am. Math. Soc. 122(1994), 885–891. https://doi.org/10.2307/2160768 CrossRefGoogle Scholar
Roberts, J. H., The rational points in Hilbert space . Duke Math. J. 23(1956), 488–491.CrossRefGoogle Scholar
Tymchatyn, E. D., Compactifications of rational spaces . Houston J. Math. 3(1977), 131–139.Google Scholar