Article contents
Injective modules over the Jacobson algebra 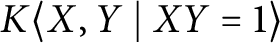 $K\langle X, Y \ | \ XY=1\rangle $
$K\langle X, Y \ | \ XY=1\rangle $
Published online by Cambridge University Press: 22 June 2020
Abstract
For a field K, let 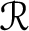 $\mathcal {R}$
denote the Jacobson algebra
$\mathcal {R}$
denote the Jacobson algebra 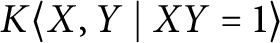 $K\langle X, Y \ | \ XY=1\rangle $
. We give an explicit construction of the injective envelope of each of the (infinitely many) simple left
$K\langle X, Y \ | \ XY=1\rangle $
. We give an explicit construction of the injective envelope of each of the (infinitely many) simple left 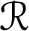 $\mathcal {R}$
-modules. Consequently, we obtain an explicit description of a minimal injective cogenerator for
$\mathcal {R}$
-modules. Consequently, we obtain an explicit description of a minimal injective cogenerator for 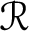 $\mathcal {R}$
. Our approach involves realizing
$\mathcal {R}$
. Our approach involves realizing 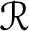 $\mathcal {R}$
up to isomorphism as the Leavitt path K-algebra of an appropriate graph
$\mathcal {R}$
up to isomorphism as the Leavitt path K-algebra of an appropriate graph 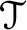 $\mathcal {T}$
, which thereby allows us to utilize important machinery developed for that class of algebras.
$\mathcal {T}$
, which thereby allows us to utilize important machinery developed for that class of algebras.
Keywords
MSC classification
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2020
References
- 1
- Cited by



