Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-25T18:25:41.316Z Has data issue: false hasContentIssue false
  • English
  • Français

Hyperbolic metric and membership of conformal maps in the Bergman space

Part of: Spaces and algebras of analytic functions Riemann surfaces Geometric function theory

Published online by Cambridge University Press:  06 May 2020

Dimitrios Betsakos ,
Christina Karafyllia  and
Nikolaos Karamanlis
Dimitrios Betsakos
Affiliation:
Department of Mathematics, Aristotle University of Thessaloniki, 54124Thessaloniki, Greece e-mail: [email protected]
Christina Karafyllia
Affiliation:
Institute for Mathematical Sciences, Stony Brook University, Stony Brook, New York 11794-3651 e-mail: [email protected]
Nikolaos Karamanlis*
Affiliation:
Department of Mathematics, Aristotle University of Thessaloniki, 54124Thessaloniki, Greece e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove that for $0<p<+\infty $ and 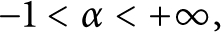$-1<\alpha <+\infty ,$ a conformal map defined on the unit disk belongs to the weighted Bergman space 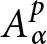$A_{\alpha }^p$ if and only if a certain integral involving the hyperbolic distance converges.

Keywords

Bergman spacehyperbolic distanceGreen functionconformal mapping

MSC classification

Primary: 30H20: Bergman spaces, Fock spaces
Secondary: 30F45: Conformal metrics (hyperbolic, Poincaré, distance functions) 30C35: General theory of conformal mappings
Type
Article
Information
Canadian Mathematical Bulletin , Volume 64 , Issue 1 , March 2021 , pp. 174 - 181
Check for updates
Copyright
© Canadian Mathematical Society 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This research was co-financed by Greece and the European Union (European Social Fund-ESF) through the Operational Programme “Human Resources Development, Education and Lifelong Learning 2014–2020” in the context of the project “Angular derivatives and the hyperbolic metric” (MIS 5047551).

References

Ahlfors, L.V., Conformal invariants: topics in geometric function theory. McGraw-Hill, New York, 1973.Google Scholar
Girela, D., Baernstein, A. and Peláez, J.Á., Univalent functions, Hardy spaces and spaces of Dirichlet type. Illinois J. Math. 48(2004), 837–859.Google Scholar
Beardon, A. F. and Minda, D., The hyperbolic metric and geometric function theory. In: Quasiconformal mappings and their applications, Narosa, New Delhi (2007), pp. 9–56.Google Scholar
Duren, P. and Schuster, A., Bergman spaces. Mathematical Surveys and Monographs, 100, American Mathematical Society, Providence, RI, 2004. https://doi.org/10.1090/surv/100CrossRefGoogle Scholar
Garnett, J. B. and Marshall, D. E., Harmonic measure. New Mathematical Monographs, 2, Cambridge University Press, Cambridge, 2005. https://doi.org/10.1017/CB09780511546617Google Scholar
Hardy, G. H. and Littlewood, J. E., Some properties of fractional integrals II. Math. Z. 34(1932), 403–439. https://doi.org/10.1007/BF01180596CrossRefGoogle Scholar
Korenblum, B. Hedenmalm, H. and Zhu, K., Theory of Bergman spaces. Graduate Texts in Mathematics, 199, Springer-Verlag, New York, 2000. https://doi.org/10.1007/978-1-4612-0497-8Google Scholar
Karafyllia, C., Hyperbolic distance and membership of conformal maps in the Hardy space. Proc. Amer. Math. Soc. 147(2019), 3855–3858.CrossRefGoogle Scholar
Kraus, D. and Roth, O., Conformal metrics. In: Topics in modern function theory, Ramanujan Math. Soc. Lect. Notes Ser. 19(2013), 41–83. https://doi.org/10.1090/proc/14512Google Scholar
Pérez-González, F. and Rättyä, J., Univalent functions in Hardy, Bergman, Bloch and related spaces. J. Anal. Math. 105(2008), 125–148. https://doi.org/10.1007/s11854-008-0032-6CrossRefGoogle Scholar
Poggi-Corradini, P., Geometric models, iteration, and composition operators. Ph.D. thesis, University of Washington (1996).Google Scholar
Pommerenke, C., Schlichte Funktionen and analytische Funktionen von beschränkten mittlerer Oszillation. Comment. Math. Helv. 52(1997), 591–602. https://doi.org/10.1007/BF02567392CrossRefGoogle Scholar
Prawitz, H., Über Mittelwerte analytischer Funktionen. Ark. Mat. Astr. Fys. 20(1927), 1–12.Google Scholar
Smith, W., Composition operators between Bergman and Hardy spaces. Trans. Amer. Math. Soc. 348 (1996), 2331–2348. https://doi.org/10.1090/S0002-9947-96-01647-9CrossRefGoogle Scholar
Stromberg, K.R., Introduction to classical real analysis. Wadsworth International Mathematics Series, Wadsworth International, Belmont, CA, 1981.Google Scholar
Zhu, K., Translating inequalities between Hardy and Bergman spaces. Amer. Math. Monthly, 111 (2004), 520–525. https://doi.org/10.2307/4145071CrossRefGoogle Scholar