Hostname: page-component-6bf8c574d5-9nwgx Total loading time: 0 Render date: 2025-02-14T10:44:51.780Z Has data issue: false hasContentIssue false
  • English
  • Français

Hilbert rings with maximal ideals of different heights and unruly Hilbert rings

Part of: Ring extensions and related topics Arithmetic rings and other special rings General commutative ring theory

Published online by Cambridge University Press:  10 March 2022

Y. Azimi
Y. Azimi*
Affiliation:
Department of Mathematics, University of Tabriz, Tabriz, Iran and Iran School of Mathematics, Institute for Research in Fundamental Sciences (IPM), Tehran, Iran
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 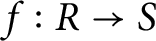$f:R\to S$ be a ring homomorphism and J be an ideal of S. Then the subring 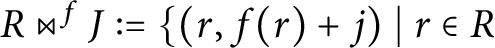$R\bowtie ^fJ:=\{(r,f(r)+j)\mid r\in R$ and 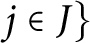$j\in J\}$ of $R\times S$ is called the amalgamation of R with S along J with respect to f. In this paper, we characterize when 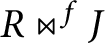$R\bowtie ^fJ$ is a Hilbert ring. As an application, we provide an example of Hilbert ring with maximal ideals of different heights. We also construct non-Noetherian Hilbert rings whose maximal ideals are all finitely generated (unruly Hilbert rings).

Keywords

Amalgamated algebraHilbert ringpullbacktrivial extension

MSC classification

Primary: 13A15: Ideals; multiplicative ideal theory
Secondary: 13B99: None of the above, but in this section 13F20: Polynomial rings and ideals; rings of integer-valued polynomials
Type
Article
Information
Canadian Mathematical Bulletin , Volume 66 , Issue 1 , March 2023 , pp. 196 - 203
Check for updates
Copyright
© Canadian Mathematical Society, 2022

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This research was in part supported by a grant from IPM (No.14001300114)

References

Anderson, D. D., Anderson, D. F., and Zafrullah, M., Rings between $D\left[X\right]$ and $K\left[X\right]$ . Houston J. Math. 17(1991), 109–129.Google Scholar
Anderson, D. D., Bennis, D., Fahid, B., and Shaiea, A., On n-trivial extensions of rings . Rocky Mountain J. Math. 47(2017), 2439–2511.CrossRefGoogle Scholar
Anderson, D. D. and Winders, M., Idealization of a module . J. Commut. Algebra 1(2009), 3–56.CrossRefGoogle Scholar
Anderson, D. F., Dobbs, D. E., and Fontana, M., Hilbert rings arising as pullbacks . Canad. Math. Bull. 35(1992), no. 4, 431–438.CrossRefGoogle Scholar
Azimi, Y., Constructing (non-)Catenarian rings . J. Algebra 597(2022), 266–274.CrossRefGoogle Scholar
Azimi, Y., Sahandi, P., and Shirmihammadi, N., Cohen–Macaulay properties under the amalgamated construction . J. Commut. Algebra 10(2018), no. 4, 457–474.CrossRefGoogle Scholar
Azimi, Y., Sahandi, P., and Shirmihammadi, N., Cohen–Macaulayness of amalgamated algebras . J. Algebra Represent. Theory 23(2019), 275–280.CrossRefGoogle Scholar
Azimi, Y., Sahandi, P., and Shirmohammadi, N., Prüfer conditions under the amalgamated construction . Comm. Algebra 47(2019), 2251–2261.CrossRefGoogle Scholar
D’Anna, M., Finocchiaro, C. A., and Fontana, M., Amalgamated algebras along an ideal . In: Commutative algebra and its applications: proceedings of the fifth international fez conference on commutative algebra and its applications, Fez, Morocco, 2008, De Gruyter, Berlin, 2009, pp. 155–172.CrossRefGoogle Scholar
D’Anna, M., Finocchiaro, C. A., and Fontana, M., Properties of chains of prime ideals in an amalgamated algebra along an ideal . J. Pure Appl. Algebra 214(2010), 1633–1641.CrossRefGoogle Scholar
D’Anna, M., Finocchiaro, C. A., and Fontana, M., New algebraic properties of an amalgamated algebra along an ideal . Comm. Algebra 44(2016), 1836–1851.CrossRefGoogle Scholar
D’Anna, M. and Fontana, M., An amalgamated duplication of a ring along an ideal: the basic properties . J. Algebra Appl. 6(2007), no. 3, 443–459.CrossRefGoogle Scholar
Finocchiaro, C. A., Prüfer-like conditions on an amalgamated algebra along an ideal . Houston J. Math. 40(2014), 63–79.Google Scholar
Gilmer, R. and Heinzer, W., A non-Noetherian two-dimensional Hilbert domain with principal maximal ideals . Michigan Math. J. 23(1976), 353–362.CrossRefGoogle Scholar
Heinzer, W., Hilbert integral domains with maximal ideals of preassigned height . J. Algebra 29(1974), 229–231.CrossRefGoogle Scholar
Kaplansky, I., Commutative rings, revised ed., University of Chicago Press, Chicago, 1974.Google Scholar
Mott, J. L. and Zafrullah, M., Unruly Hilbert domains . Canad. Math. Bull. 33(1990), 106–109.CrossRefGoogle Scholar
Nagata, M., Local rings, Interscience, New York, 1962.Google Scholar
Roberts, L., An example of a Hilbert ring with maximal ideals of different heights . Proc. Amer. Math. Soc. 37(1973), 425–426.CrossRefGoogle Scholar
Sahandi, P., Shirmohammadi, N., and Sohrabi, S., Cohen–Macaulay and Gorenstein properties under the amalgamated construction . Comm. Algebra 44(2016), 1096–1109.CrossRefGoogle Scholar