Hostname: page-component-6bf8c574d5-956mj Total loading time: 0 Render date: 2025-02-23T14:28:55.289Z Has data issue: false hasContentIssue false
  • English
  • Français

Embedding of some classes of operators into strongly continuous semigroups

Part of: Groups and semigroups of linear operators, their generalizations and applications Special classes of linear operators

Published online by Cambridge University Press:  08 January 2025

Isabelle Chalendar  and
Romain Lebreton
Isabelle Chalendar*
Affiliation:
Université Gustave Eiffel, LAMA (UMR 8050), UPEM, UPEC, CNRS, F-77454 Marne-la-Vallée, France
Romain Lebreton
Affiliation:
Laboratoire Paul Painlevé, Université de Lille, 59655 Villeneuve d’Ascq Cédex France e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we study the embedding problem of an operator into a strongly continous semigroup. We obtain characterizations for some classes of operators, namely composition operators and analytic Toeplitz operators on the Hardy space 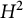$H^2$. In particular, we focus on the isometric ones using the necessary and sufficient condition observed by T. Eisner.

Keywords

Semigroupembeddingisometrycomposition operatorToeplitz operator

MSC classification

Primary: 47D03: Groups and semigroups of linear operators 47B33: Composition operators 47B35: Toeplitz operators, Hankel operators, Wiener-Hopf operators
Type
Article
Information
Canadian Mathematical Bulletin , Volume 68 , Issue 1 , March 2025 , pp. 219 - 231
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Al Alam, I., Chalendar, I., El Chami, F., Fricain, E., and Lefèvre, P., Eventual ideal properties of the Riemann–Liouville analytic semigroup. Preprint, 2024. arXiv:2404.19540 [math.FA].Google Scholar
Arendt, W., Batty, C. J. K., Hieber, M., and Neubrander, F., Vector-valued Laplace transforms and Cauchy problems, Monographs in Mathematics, 96, Birkhäuser Verlag, Basel, 2001.CrossRefGoogle Scholar
Arendt, W., Chalendar, I., Kumar, M., and Srivastava, S., Powers of composition operators: asymptotic behaviour on Bergman, Dirichlet and Bloch spaces . J. Aust. Math. Soc. 108(2020), no. 3, 289–320.CrossRefGoogle Scholar
Bayart, F., Similarity to an isometry of a composition operator . Proc. Amer. Math. Soc. 131(2003), no. 6, 1789–1791.CrossRefGoogle Scholar
Bracci, F., Contreras, M. D., and Díaz-Madrigal, S., Infinitesimal generators associated with semigroups of linear fractional maps . J. Anal. Math. 102(2007), 119–142.CrossRefGoogle Scholar
Bracci, F., Contreras, M. D., and Díaz-Madrigal, S., Continuous semigroups of holomorphic self-maps of the unit disc, Springer Monographs in Mathematics, Springer, Cham, 2020.CrossRefGoogle Scholar
Celariès, B. and Chalendar, I., Three-lines proofs on semigroups of composition operators. Ulmer Seminare 2016/2017, vol. 20, 2017.Google Scholar
Chalendar, I. and Partington, J. R., Weighted composition operators: isometries and asymptotic behaviour . J. Operator Theory 86(2021), no. 1, 189–201.CrossRefGoogle Scholar
Eisner, T., Embedding operators into strongly continuous semigroups . Arch. Math. (Basel) 92(2009), no. 5, 451–460.CrossRefGoogle Scholar
Eisner, T., Stability of operators and operator semigroups, Operator Theory: Advances and Applications, 209, Birkhäuser Verlag, Basel, 2010.CrossRefGoogle Scholar
Engel, K.-J. and Nagel, R., A short course on operator semigroups, Universitext, Springer, New York, 2006.Google Scholar
Garcia, S. R., Mashreghi, J., and Ross, W. T., Introduction to model spaces and their operators, Cambridge Studies in Advanced Mathematics, 148, Cambridge University Press, Cambridge, 2016.CrossRefGoogle Scholar
Garcia, S. R., Mashreghi, J., and Ross, W. T., Finite Blaschke products: A survey . In: Harmonic analysis, function theory, operator theory, and their applications, Theta Ser. Adv. Math., 19, Theta, Bucharest, 2017.Google Scholar
Kumar, R. and Partington, J. R., Weighted composition operators on Hardy and Bergman spaces . In: Recent advances in operator theory, operator algebras, and their applications, Operator Theory: Advances and Applications, 153, Birkhäuser, Basel, 2005, pp. 157–167.Google Scholar
Nordgren, E. A., Composition operators . Canad. J. Math. 20(1968), 442–449.CrossRefGoogle Scholar
Seubert, S. M., Semigroups of analytic Toeplitz operators on ${H}^2$ . Houston J. Math. 30(2004), no. 1, 137–145.Google Scholar
Shapiro, J. H., Composition operators and classical function theory, Universitext: Tracts in Mathematics, Springer-Verlag, New York, 1993.CrossRefGoogle Scholar