No CrossRef data available.
Article contents
Abelian Theorems for Hardy Transformations
Published online by Cambridge University Press: 20 November 2018
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Initial and final value theorems for Hardy transformations 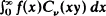 and
and 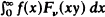 of a suitably chosen function f(x) under a certain set of conditions on v and p where
of a suitably chosen function f(x) under a certain set of conditions on v and p where
1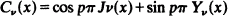
Jv(x) and Yv(x) being Bessel functions of the first and second kind, and
2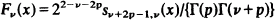
su, v(x) being Lommel's function, are proved.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1977
References
1.
Cooke, R. G., The inversion formulae of Hardy and Titchmarsh. Proc. London Math. Soc.
24 (1925), 381-420.Google Scholar
2.
Erdély, A., (Editor). Tables of integral transforms, Vol. I (McGraw-Hill Book Co., Inc., New York, 1954).Google Scholar
3.
Erdély, A., (Editor). Tables of integral transforms, Vol. II (McGraw-Hill Book Co., Inc., New York, 1954).Google Scholar
4.
Hardy, G. H., Some formulae in the theory of Bessel functions. Proc. London Math. Soc.
23 (1925), lxi-lxiii.Google Scholar
5.
Pathak, R. S., and Pandey, J. N., A distributional Hardy transformation. Proc. Camb. Phil. Soc.
76 (1974), 247-262.
Google Scholar
6.
Pathak, R. S., and Pandey, J. N., A distributional Hardy transformation II. Submitted for publication.Google Scholar
7.
Watson, G. N., A treatise on the theory of Bessel functions (Cambridge University Press, second edn., 1962).Google Scholar
9.
Zemanian, A. H., Some abelian theorems for the Distributional Hankel and K transformations, SIAM J. Appl. Math., Vol. 14 (1966), 1106-1111.Google Scholar


