Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Blair, David E.
2000.
Vol. 1,
Issue. ,
p.
153.
PARK, Joon-Sik
2005.
Critical Homogeneous Metrics on the Heisenberg Manifold.
Interdisciplinary Information Sciences,
Vol. 11,
Issue. 1,
p.
31.
Pyo, Yong-Soo
Kim, Hyun-Woong
and
Park, Joon-Sik
2010.
ON STABILITY OF EINSTEIN WARPED PRODUCT MANIFOLDS.
Honam Mathematical Journal,
Vol. 32,
Issue. 1,
p.
167.
Park, Joon-Sik
2014.
A DECOMPOSITION OF THE CURVATURE TENSOR FIELD ON THE ABBENA-THURSTON MANIFOLD.
Honam Mathematical Journal,
Vol. 36,
Issue. 4,
p.
795.
Han, Ju-Wan
Kim, Hyun Woong
and
Pyo, Yong-Soo
2016.
CURVATURES ON THE ABBENA-THURSTON MANIFOLD.
Honam Mathematical Journal,
Vol. 38,
Issue. 2,
p.
359.
Son, Heui-Sang
Kim, Hyun Woong
and
Park, Joon-Sik
2016.
HARMONIC HOMOMORPHISMS BETWEEN TWO LIE GROUPS.
Honam Mathematical Journal,
Vol. 38,
Issue. 1,
p.
1.
Park, Joon-Sik
2016.
DIFFERENTIAL GEOMETRIC PROPERTIES ON THE HEISENBERG GROUP.
Journal of the Korean Mathematical Society,
Vol. 53,
Issue. 5,
p.
1149.


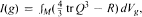 where
where 