Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-07T15:09:55.521Z Has data issue: false hasContentIssue false
  • English
  • Français

2-Primary Exponent Bounds for Lie Groups of Low Rank

Published online by Cambridge University Press:  20 November 2018

Stephen D. Theriault
Stephen D. Theriault*
Affiliation:
Department of Mathematics University of Virginia Charlottesville, VA 22904 USA
*
Current address: Department of Mathematical Sciences University of Aberdeen Aberdeen AB24 3UE United Kingdom, email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Exponent information is proven about the Lie groups 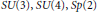$SU(3),\,SU(4),\,Sp(2)$, and 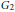${{G}_{2}}$ by showing some power of the 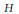$H$-space squaring map (on a suitably looped connected-cover) is null homotopic. The upper bounds obtained are 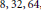$8,\,32,\,64$, and 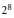${{2}^{8}}$ respectively. This null homotopy is best possible for $SU(3)$ given the number of loops, off by at most one power of 2 for $SU(4)$ and 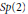$Sp(2)$, and off by at most two powers of 2 for 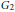${{G}_{2}}$.

Keywords

55Q52Lie groupexponent
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 47 , Issue 1 , 01 March 2004 , pp. 119 - 132
Copyright
Copyright © Canadian Mathematical Society 2004

References

[C1] Cohen, F. R., A short course in some aspects of classical homotopy theory. Lecture Notes in Math. 1286, Springer-Verlag, 1987, 1–92.Google Scholar
[C2] Cohen, F. R., Applications of loop spaces to some problems in topology. London Math. Soc. Lecture Notes Series 139 (1989), 11–20.Google Scholar
[DM1] Davis, D. M. and Mahowald, M., Three contributions to the homotopy theory of the exceptional Lie groups G2 and F4 . J. Math. Soc. Japan 43 (1991), 661–671.Google Scholar
[DM2] Davis, D. M. and Mahowald, M., Some remarks on v1-periodic homotopy groups. LondonMath. Soc. Lecture Notes Series 176 (1992), 55–72.Google Scholar
[M] Mimura, M., The homotopy groups of Lie groups of low rank. J. Math. Kyoto Univ. 6 (1967), 131–176.Google Scholar
[MT] Mimura, M. and Toda, H., Homotopy groups of SU(3), SU(4), and Sp(2). J. Math. Kyoto Univ. 3 (1964), 217–250.Google Scholar
[N] Neisendorfer, J. A., Properties of certain H-spaces. Quart. J. Math. Oxford 34 (1983), 201–209.Google Scholar
[R] Richter, W., The H-space squaring map on Ω3S4n+1 factors through the double suspension. Proc. Amer.Math. Soc. 123 (1995), 3889–3900.Google Scholar