Hostname: page-component-745bb68f8f-d8cs5 Total loading time: 0 Render date: 2025-02-10T09:17:42.429Z Has data issue: false hasContentIssue false
  • English
  • Français

2-Clean Rings

Published online by Cambridge University Press:  20 November 2018

Z. Wang  and
J. L. Chen
Z. Wang
Affiliation:
Department of Mathematics, Southeast University, Nanjing, 210096, China e-mail: [email protected]@seu.edu.cn
J. L. Chen
Affiliation:
Department of Mathematics, Southeast University, Nanjing, 210096, China e-mail: [email protected]@seu.edu.cn
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

$\text{A}$ ring $R$ is said to be $n$-clean if every element can be written as a sum of an idempotent and $n$ units. The class of these rings contains clean rings and $n$-good rings in which each element is a sum of $n$ units. In this paper, we show that for any ring $R$, the endomorphism ring of a free $R$-module of rank at least 2 is 2-clean and that the ring 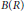$B\left( R \right)$ of all $\omega \,\times \,\omega$ row and column-finite matrices over any ring $R$ is 2-clean. Finally, the group ring 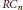$R{{C}_{n}}$ is considered where $R$ is a local ring.

Keywords

16D7016D4016S502-clean rings2-good ringsfree modulesrow and column-finite matrix ringsgroup rings
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 52 , Issue 1 , 01 March 2009 , pp. 145 - 153
Copyright
Copyright © Canadian Mathematical Society 2009

References

[1] Camillo, V. P. and Yu, H.-P., Exchange rings, units and idempotents. Comm. Algebra 22(1994), no. 12, 4737–4749.Google Scholar
[2] Castagna, F., Sums of automorphisms of a primary abelian group. Pacific J. Math. 27(1968), 463–473.Google Scholar
[3] Fisher, J. W. and Snider, R. L., Rings generated by their units. J. Algebra 42(1976), no. 2, 363–368.Google Scholar
[4] Goldsmith, B., On endomorphisms and automorphisms of some torsion-free modules. Abelian Group Theory (Oberwolfach, 1985), Gordon and Breach, New York, 1987, 417–423.Google Scholar
[5] Goldsmith, B., Pabst, S., and Scott, A., Unit sum numbers of rings and modules. Quart. J. Math. Oxford Ser. (2) 49(1998), no. 195, 331–344.Google Scholar
[6] Han, J. and Nicholson, W. K., Extensions of clean rings. Comm. Algebra 29(2001), no. 6, 2589–2595.Google Scholar
[7] Henriksen, M., Two classes of rings generated by their units. J. Algebra 31(1974), 182–193.Google Scholar
[8] Hill, P., Endomorphism rings generated by units. Trans. Amer. Math. Soc. 141(1969), 99–105.Google Scholar
[9] Meehan, C., Sums of automorphisms of free abelian groups and modules. Math. Proc. R. Ir. Acad. 104A(2004), no. 1, 59–66.Google Scholar
[10] Meehan, C., Sums of automorphisms of free modules and completely decomposable groups. J. Algebra 299(2006), no. 2, 467–479.Google Scholar
[11] Nicholson, W. K., Local group rings. Canad. Math. Bull. 15(1972), 137–138.Google Scholar
[12] Nicholson, W. K., Lifting idempotents and exchange rings. Trans. Amer. Math. Soc. 229(1977), 269–278.Google Scholar
[13] O’Meara, K. C., The exchange property for row and column-finite matrix rings. J. Algebra 268(2003), no. 2, 744–749.Google Scholar
[14] Raphael, R., Rings which are generated by their units. J. Algebra 28(1974), 199–205.Google Scholar
[15] Vámos, P., 2-good rings. Q. J. Math. 56(2005), no. 3, 417–430.Google Scholar
[16] Wans, C., Summen von Automorphismen freierModuln. Ph.D. Thesis, Universität Essen, 1995.Google Scholar
[17] Wolfson, K. G., An ideal-theoretic characterization of the ring of all linear transformations. Amer. J. Math. 75(1953), 358–386.Google Scholar
[18] Woods, S. M., Some results on semi-perfect group rings. Canad. J. Math. 26(1974), 121–129.Google Scholar
[19] Xiao, G. and Tong, W., n-clean rings and weakly unit stable range rings. Comm. Algebra 33(2005), no. 5, 1501–1517.Google Scholar
[20] Zelinsky, D., Every linear transformation is a sum of nonsingular ones. Proc. Amer. Math. Soc. 5(1954), 627–630.Google Scholar