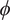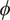Reductive Views of Knowledge and the Small Difference Principle

Abstract

I develop a challenge to reductive views of knowing that $ \phi $ that appeal to what I call a gradable property. Such appeal allows for properties that are intrinsically very similar to the property of knowing that $ \phi $, but differ significantly in their normative significance. This violates the independently plausible claim Pautz (2017) labels the ‘small difference principle.’

1. Introduction

Can we reduce the property of knowing that $ \phi $ to another property? My aim here is to challenge purported reductions that appeal to a gradable property. The core issue is that use of such a property in attempted reductions entails the existence of properties that are intrinsically very similar to knowing that $ \phi $ , but differ significantly in their normative significance. This violates what Pautz (2017, 368) calls the ‘small difference principle’ (to a first approximation, the claim that for any two intrinsically very similar properties, if one is normatively significant in some way, then the other is normatively significant in a similar way). Absent evidence against the principle, we thus have reason to reject reductive views that appeal to a gradable property.

Section 2 identifies the class of reductive views I target; section 3 discusses Pautz’s small difference principle; section 4 sketches some ways in which knowing that $ \phi $ is normatively significant; section 5 states the challenge and replies to two objections; section 6 concludes by sketching a nonreductive view that avoids my challenge.

2. Reductive views

A view of some entity e is reductive only if it entails that e is no addition to our ontology. To entail this, a view must either say that e does not exist or identify e with some other entity already included in our ontology. A view corresponding to the first disjunct eliminates e; one corresponding to the second reduces it. Hence, a reductive view of the property of knowing that $ \phi $ identifies it with another property (which may itself be built from further properties)—its reduction base.

My challenge targets all reductive views whose reduction bases involve a gradable property. My use of the term ‘gradable’ does not correspond to its current (technical) use by linguists and philosophers of language to describe ‘gradable’ adjectives. That is, expressions of gradable properties as I use the term need not (though they may) pass linguistic tests for gradable adjectives, such as the admissibility of comparative constructions (‘x is flatter than y,’ ‘x is as boring as y’), degree-‘how’-questions (‘how tall is x?’), and degree modifiers (‘x is somewhat bent,’ ‘x is completely insane,’ etc.). The core feature shared by what I call gradable properties is that they correspond to a certain kind of ordering along which any two adjacent properties are intrinsically very similar. As an example, consider the property of being regarded by Ayesha as 0.9 likely. This is a gradable property insofar as it corresponds to an ordering along which any two adjacent properties are intrinsically very similar: an ordering by degree of likelihood. Being regarded by Ayesha as 0.9 likely and being regarded by Ayesha as 0.900001 likely are not only (roughly) adjacent in this ordering, but also intrinsically very similar; and so on for other degrees of likelihood.

As I use the term, two properties are intrinsically very similar just in case they are very similar in virtue of the way they themselves are. Importantly, two properties may be intrinsically very similar in this sense even if neither of these properties is intrinsic. For instance, the properties of being regarded by Ayesha as 0.9 likely and of being regarded by Ayesha as 0.900001 likely are extrinsic: a proposition isn’t regarded as so-and-so likely by someone just in virtue of the way that proposition itself, and nothing else, is. Yet these properties are intrinsically very similar because they’re very similar just in virtue of the way these properties by themselves are. The possibility of two properties being intrinsically very similar even if neither of them is intrinsic is important, because no plausible reduction base for knowing that $ \phi $ is an intrinsic property. Cases of self-knowledge aside, for one to have knowledge that $ \phi $ requires one’s environment to be a certain way.

Let’s turn to four putative reduction bases for the property of knowing that $ \phi $ which appeal to a gradable property and so are subject to my challenge. ¹ First, the evidence reduction base (inspired by, e.g., Schaffer and Szabó 2014): the property of truly believing that $ \phi $ based on maximally or at least sufficiently strong evidence for $ \phi $ . ² This reduction base involves a property that corresponds to an ordering by degree of strength, since one’s evidence for $ \phi $ may be stronger or weaker. ³ Knowledge-generating evidence just is found fairly high up in, or at the very top of, the ordering. Moreover, any two properties adjacent along this ordering, very roughly truly believing that $ \phi $ based on evidence of strength n and truly believing that $ \phi $ based on evidence of strength $ n-1 $ / $ n+1 $ , are intrinsically very similar. So, this reduction base involves a gradable property.

Second, consider the reliability reduction base (see Goldman 1986, 51; Goodman and Salow 2018): the property of believing that $ \phi $ via a maximally or at least sufficiently reliable method. ⁴ Since a method of belief formation can be more or less reliable, the reliability reduction base involves a property that corresponds to an ordering by degree of reliability. Knowledge-generating methods of belief formation just are ones placed fairly high up in, or at the very top of, the ordering. Moreover, any two properties adjacent along this ordering, very roughly truly believing that $ \phi $ via a method reliable to degree n and truly believing that $ \phi $ via a method reliable to degree $ n-1 $ / $ n+1 $ , are intrinsically very similar. So, the reliability reduction base too involves a gradable property

Third, take the safety reduction base (see Ball 2013; Peet and Pitcovski 2018): the property of safely believing that $ \phi $ , where to safely believe that $ \phi $ at a world w is (abstracting from methods of belief formation) for $ \phi $ to be true at all or at least at sufficiently many of the closest worlds at which one believes that $ \phi $ . ⁵ Safe belief thus defined does not admit of the degree modifiers more or less; either one truly believes that $ \phi $ at all/sufficiently many of the closest worlds or one doesn’t. However, to safely believe that $ \phi $ is to truly believe that $ \phi $ throughout a certain region of modal space. And one can truly believe that $ \phi $ throughout a larger or smaller region of modal space. Thus, this reduction base involves a property that corresponds to an ordering by the size of the region of modal space throughout which one truly believes that $ \phi $ . Moreover, any two properties adjacent along this ordering, truly believing that $ \phi $ throughout region of modal space K and truly believing that $ \phi $ throughout K minus/plus some world at K’s border, are intrinsically very similar. So, the safety reduction base also involves a gradable property.

Finally, consider the virtue reduction base (see Sosa 2007): the property of aptly believing that $ \phi $ , where to aptly believe that $ \phi $ is for one’s belief to be true because it is competent, and for a belief to be competent is for it to be produced by an exercise of an ability to form true beliefs. Whether this reduction base involves a gradable property, as I use the term, depends on how we characterise an ability to form true beliefs; but on the view of its most prominent defender, it does. Sosa (2007, 29) writes that an ability to form true beliefs is “a disposition […] that would in appropriately normal conditions ensure (or make highly likely) the success of any relevant performance issued by it.” Given this, aptly believing that $ \phi $ involves a property gradable across two dimensions. First, a disposition can ensure (or make highly likely) success in a larger or smaller range of conditions. This gives an ordering by the size of a region of modal space, namely that region throughout which a disposition ensures (or makes highly likely) success. Second, at any point in the relevant region of modal space, the disposition can make more or less likely the success of the performance issued from it. This yields an ordering by degree of probability. Moreover, any two properties adjacent on either of these orderings, for instance truly believing that $ \phi $ because one’s belief is produced by a disposition that ensures success in conditions $ {c}_1\dots {c}_n $ and truly believing that $ \phi $ because one’s belief is produced by a disposition that ensures success in conditions $ {c}_1\dots {c}_n $ minus/plus some $ {c}_i $ , are intrinsically very similar. Thus, the virtue reduction base, at least as understood by Sosa, involves a gradable property.

As I formulated them, all four reduction bases admit of both fallibilist and infallibilist variants. For instance, the evidence reduction base may involve either having maximally, or sufficiently, strong evidence (where sufficiency will normally fall below the maximal level). Extant discussion of the threshold problem for fallibilist views of knowledge (BonJour 2010; Climenhaga 2021)—the problem of setting a threshold for sufficiently strong evidence that vindicates the value of knowledge—might lead us to expect that infallibilism avoids my challenge. However, that expectation is mistaken. For even maximally strong evidence is evidence of some strength and thus involves a gradable property.

To illustrate this, suppose maximally strong evidence is truth-entailing evidence: having maximally strong evidence for $ \phi $ thus entails that $ \phi $ . Admittedly, this evidence differs significantly from less than maximally strong evidence since the latter doesn’t entail that $ \phi $ . But consider what truth-entailing evidence is—at least given a standard model-theoretic definition of entailment: it is evidence such that all of the cases at which one possesses this evidence are cases at which $ \phi $ is true. Thus, having truth-entailing evidence is a gradable property just as safety is: it is a property that corresponds to an ordering by the size of the region of “case space” throughout which $ \phi $ is true. Moreover, any two properties adjacent along this ordering, $ \phi $ being true throughout region of case space K and $ \phi $ being true throughout K minus some case at K’s border, are intrinsically very similar. Consequently, infallibilists are no better off than fallibilists in dealing with my challenge. ⁶

Now, all reduction bases considered so far involved the property of believing that $ \phi $ . However, my challenge arises also if we substitute ‘accepting that $ \phi $ ,’ ‘holding true that $ \phi $ ,’ ‘being sure that $ \phi $ ,’ etc. for ‘believing that $ \phi $ ’ as it occurs in the reduction bases above. ⁷ More generally, my challenge arises for all reductive views of knowing that $ \phi $ whose reduction base involves a gradable property, whether or not they appeal to any of the properties mentioned so far.

Admittedly, this does not mean that my challenge arises for reductive views as such. But it does mean that the challenge arises for a very wide range of views. To see how far the challenge might generalise, consider, for instance, the reduction base proposed by Hyman (1999), on which to know that $ \phi $ is to be able to A for the reason that $ \phi $ , where A ranges over actions (like ice skating) and attitudes (like believing). At first glance at least, this reduction base too involves a gradable property. For it seems that one’s ability to A for the reason that $ \phi $ might be better or worse where this might involve, for instance, differences in the size of the region of modal space throughout which one succeeds at A ing for the reason that $ \phi $ . Yet again then, we get an ordering by the size of a region of modal space. Moreover, any two properties adjacent in the resulting ordering, for instance succeeding at Aing for the reason that $ \phi $ throughout region of modal space K and succeeding at Aing for the reason that $ \phi $ throughout K minus a world at K’s border, are intrinsically very similar. Thus, this reduction base too involves, at least at first glance, a gradable property. So, despite being radically different from the belief-based views mentioned previously, Hyman’s view might well face my challenge.

3. The small difference principle

My challenge turns on Pautz’s (2017) small difference principle; so let’s start with two cases, adapted from Pautz’s discussion, from which we can generalise to the principle. After that I’ll discuss three concerns for the small difference principle, two of which will require refining the principle.

As a first example, consider pains. They can be more or less intense. This generates an ordering along which any two adjacent properties are intrinsically very similar. Consider, for instance, ‘pain-17,’ a very strong pain, and ‘pain-16,’ a pain just one unit of strength weaker than pain-17. Pain-17 has a normative significance because undergoing it immediately grounds a pro tanto reason to want it to stop; moreover, the strength of that reason corresponds (roughly) to the strength of one’s pain. Because pain-16 is just one unit of strength weaker than pain-17, it would be odd to insist that undergoing it doesn’t immediately ground a pro tanto reason to want it (pain-16) to stop. One does have such a reason, and the strength of that reason is similar to that provided by pain-17, although perhaps, corresponding to the difference in strength of pain, a little weaker. Pain-17 and pain-16 thus have a similar normative significance.

Consider another example. The dyadic property of friendship appears to come in degrees. One friendship can be closer than another. This generates an ordering such that any two friendships adjacent on that ordering are intrinsically very similar. Let ‘friendship-17’ be a very close friendship. It has normative significance insofar as it immediately grounds certain pro tanto duties toward one’s friend. Now let ‘friendship-16’ be a friendship that’s just a little less close. Because friendship-16 is just a little less close than friendship-17, standing in this relation to a person immediately grounds certain pro tanto duties toward them that are similar, though perhaps not identical, to those imposed on one by friendship-17. It would be odd to insist that there is a significant normative discontinuity between friendship-17 and friendship-16; they appear to have a similar normative significance.

In the case of pain-17 and pain-16, we have two intrinsically very similar properties that have a correspondingly similar normative significance; similarly, in the case of friendship-17 and friendship-16. If we generalise from these two cases, we obtain what Pautz (2017, 368) calls the ‘small difference principle’:

1. 1. For any two ( $ n $ -adic) properties $ F $ , $ G $ and any normative significance $ N $ , if $ F $ has $ N $ and $ G $ is intrinsically very similar to $ F $ , then there is some normative significance $ {N}^{\prime } $ such that $ G $ has $ {N}^{\prime } $ and $ {N}^{\prime } $ is similar to $ N $ .

Admittedly, there are several worries we might have about this principle. For instance, we might be concerned that it licenses a version of the Sorites paradox. Take a sequence of properties $ {F}_1,{F}_2,\dots {F}_n $ such that they are pairwise intrinsically very similar ( $ {F}_1 $ is intrinsically very similar to $ {F}_2 $ , $ {F}_2 $ to $ {F}_3 $ , etc.). By the small difference principle, $ {F}_1,{F}_2,\dots {F}_n $ are pairwise of similar normative significance. Does the principle therefore predict that $ {F}_1 $ and $ {F}_n $ have similar normative significance? If so, that would be a problem: if $ {F}_1 $ is having an incredibly strong pain and $ {F}_n $ having no pain (a pain of strength 0, as one might put it), it is clear that they do not have a similar normative significance; $ {F}_1 $ immediately grounds a very strong pro tanto reason to want $ {F}_1 $ to stop, but $ {F}_n $ provides no such reason of any strength whatsoever.

Importantly, however, the principle does not make the problematic prediction. The key is that it applies to pairs of intrinsically very similar properties, and says of them merely that they have a similar normative significance. For this reason, the principle allows small intrinsic differences between properties to sum to big differences in their normative significance (399). This in turn allows $ {F}_1 $ and $ {F}_n $ in the sequence above to have very different normative significance.

A far more pressing worry for the small difference principle is that it appears subject to counterexample. Suppose I promise you to congratulate you on your birthday by 7 p.m. at the latest. My promise immediately grounds an obligation. If I do not congratulate you on your birthday before 7 p.m., I break my promise and thereby violate my obligation. Now consider two properties: congratulating you on your birthday at 7 p.m. and congratulating you on your birthday one nanosecond after 7 p.m. These two properties are intrinsically very similar: they are very similar in virtue of the way they themselves are. Yet instantiating one satisfies my obligation to you, whereas instantiating the other violates it. So, they appear to be of strikingly different, rather than similar, normative significance. Thus, they appear to be counterexamples to the small difference principle.

These examples appear to be instances of a general problem for the small difference principle. There is a wide range of acts that immediately ground an obligation to $ \phi $ such that at least some ways of failing to $ \phi $ are intrinsically very similar to $ \phi $ ing, but violate, rather than satisfy, the obligation to $ \phi $ . One type of act falling into this range is promising. If an individual promises to $ \phi $ , the normative landscape is rendered discontinuous: although $ \phi $ ing and certain ways of failing to $ \phi $ are intrinsically very similar, only $ \phi $ ing will keep the promise. Another relevant type of act, more likely to be performed by groups, is to set a norm of etiquette. If a political party, say, imposes the obligation of addressing other party members as “comrades,” the normative landscape is yet again rendered discontinuous: although satisfying this obligation and certain ways of failing to satisfy it are intrinsically very similar, only the former satisfy it.

Fortunately, the examples just mentioned do not tell against the small difference principle. This is because of the type of normative significance properties like congratulating you on your birthday at 7 p.m., congratulating you on your birthday one nanosecond after 7 p.m., etc. possess. Their normative significance contrasts with that of pain and friendship, the examples from which we generalised to obtain the small difference principle: instantiating the former properties satisfies or violates an obligation, whereas the latter immediately ground, as we might say “provide,” a reason or a duty. We can label the first type of normative significance ‘satisfaction significance,’ the latter ‘provision significance’: congratulating you on your birthday at 7 p.m. is satisfaction significant, whilst pain-16, friendship-16, and promising to congratulate you on your birthday at 7 p.m. too are provision significant. ⁸ With these labels in mind, we can read the small difference principle as concerning provision significance in particular, rather than normative significance in general. Given this, examples of satisfaction significance do not undermine the small difference principle.

Unfortunately, however, even the provision side of the normative landscape turns out to be discontinuous. Suppose, for instance, we play darts to determine who will wash the dishes and commit to the following: if and only if one hits the bull’s eye, this permits one not to wash the dishes. You hit the bull’s eye; although I almost do (just a nanometre is missing), I don’t quite manage. So, your hitting the bull’s eye immediately grounds your permission not to wash the dishes, whereas my hitting the bit just one nanometre removed from the bull’s eye doesn’t. Hitting the bull’s eye and hitting the bit one nanometre removed from the bull’s eye thus appear to have a strikingly different, rather than similar, provision significance, despite being intrinsically very similar properties.

These examples appear to be instances of yet another general problem for the small difference principle. There is a wide range of acts $ {a}_1\dots {a}_n $ that immediately ground an obligation/a permission to $ \phi $ such that at least some acts intrinsically very similar to $ {a}_1\dots {a}_n $ don’t do so. This is because individuals or groups often have the authority to stipulate that a certain condition immediately grounds an obligation/a permission. Just as the two of us stipulate that hitting the bull’s eye has a certain normative consequence for us, a club might stipulate that being at least 180 centimetres tall has a certain normative consequence for its members (an obligation to walk barefoot in the club’s premises, say), and a state might stipulate that earning at least 9000€ has a certain normative consequence for its residents (an obligation to pay income tax). In each case, the stipulation results in intrinsically very similar properties having strikingly different provision significance: neither hitting the bit one nanometre removed from the bull’s eye, nor being 179,99999 centimetres tall, nor earning 8999,99€ have the stipulated normative consequence. ⁹

Yet again, we can salvage the small difference principle by restricting it. One crucial difference between Pautz’s two examples and the counterexamples just given is that the normative significance of pain and friendship does not appear to be the result of stipulation in the way the normative significance of being 180 centimetres tall or of earning 9000€ is. No individual or group is required to stipulate that pain immediately grounds a pro tanto reason to want it to stop or to stipulate that friendship immediately grounds pro tanto duties toward one’s friend. Instead, these normative consequences of pain and friendship appear to be wholly due to what pain and friendship are; in some way these normative consequences seem essential to pain and friendship. By contrast, what hitting the bull’s eye is tells us nothing about whether it immediately grounds your permission to not wash the dishes. In light of this, we can restrict the small difference principle to provision significance that’s wholly due to what a property is:

1. 2. For any two ( $ n $ -adic) properties $ F $ , $ G $ and any provision significance $ N $ , if $ F $ has $ N $ wholly because of what $ F $ is and $ G $ is intrinsically very similar to $ F $ , then there is some provision significance $ {N}^{\prime } $ such that $ G $ has $ {N}^{\prime } $ and $ {N}^{\prime } $ is similar to $ N $ .

Given this restriction, the small difference principle requires only that provision significance that’s wholly due to what a property is be continuous and allows for the provision-side of the normative landscape to be discontinuous elsewhere.

4. Provision significance

Pain and friendship are provision significant insofar as they immediately ground pro tanto reasons and pro tanto duties respectively. In what way(s) is knowing that $ \phi $ provision significant? To streamline the argument below, it will be useful to pack slightly more into the provision significance of knowing that $ \phi $ than we did in the case of pain and friendship. The provision significance of pain and friendship consisted, in effect, of two components: they immediately ground one’s having a certain normative status; and this, in turn, means that they are a sufficient condition for that normative status. By contrast, in describing the provision significance of knowing that $ \phi $ , I mean to add another component: that knowing that $ \phi $ is, in addition to being a sufficient condition for a certain normative status, also a necessary condition for it.

As the following claims illustrate, it’s fairly common to attribute two of these three components of provision significance to knowing that $ \phi $ :

1. 3. One is permitted to believe that $ \phi $ iff one knows that $ \phi $ . ¹⁰

2. 4. One is permitted to treat $ \phi $ as a reason for acting iff one knows that $ \phi $ (Hawthorne and Stanley 2008, 578).

3. 5. A jury (objectively) ought to convict the defendant iff the jury knows that the defendant is guilty (Littlejohn 2020, 2021).

All of 3 to 5 entail that knowing that $ \phi $ is a necessary and sufficient condition on a certain normative status. Both 3 and 4 involve the normative status of being permitted; 5 involves the normative status of being obliged.

None of 3, 4, and 5, however, entail that knowing that $ \phi $ immediately grounds a certain normative status. However, in each case, this additional claim seems almost as plausible, if not just as plausible, as the biconditional does. For instance, if one knows that $ \phi $ , and so by 3 is permitted to believe that $ \phi $ , then presumably one’s permission to so believe is immediately grounded in one’s knowing that $ \phi $ ; as I’ll put it, knowing that $ \phi $ permits one to believe that $ \phi $ . Similarly, if one knows that $ \phi $ , and so by 4 is permitted to treat $ \phi $ as a reason for acting, then arguably one’s permission to do so is immediately grounded in one’s knowing that $ \phi $ ; that is, knowing that $ \phi $ permits one to treat $ \phi $ as a reason for action. Finally, if the jury knows that the defendant is guilty, then arguably its obligation to convict is immediately grounded in its knowing that the defendant is guilty; i.e., knowing that the defendant is guilty obliges the jury to convict.

The plausibility of each of these grounding claims conditional on the corresponding biconditional is at least in part due to the fact that the biconditional merely states a correlation within the “case space” that demands an explanation. Part of this explanation is provided by the grounding claims. If being F is immediately grounded in being G, then it follows that being F is a sufficient condition for being G. Thus, the grounding claims explain one direction of the biconditionals. Given this, it arguably should be, even if it isn’t, fairly common to attribute also the grounding component of provision significance to the property of knowing that $ \phi $ :

1. 6. One’s knowing that $ \phi $ permits one to believe that $ \phi $ .

2. 7. One’s knowing that $ \phi $ permits one to treat $ \phi $ as a reason for action.

3. 8. The jury’s knowing that the defendant is guilty obliges it to convict.

   Of course, 3, 4, 5, and the corresponding grounding claims are controversial (see e.g., Neta 2009; Gerken 2011; Simion, Kelp, and Ghijsen 2016). But for my purposes, that doesn’t matter too much. As long as knowledge has some other similar provision significance, that will do for my purposes. ¹¹

A question that looms large, however, is this: is any provision significance of knowing that $ \phi $ wholly due to what knowing that $ \phi $ is? Only if there’s one that is does the small difference principle predict that properties intrinsically very similar to either knowing that $ \phi $ or a property identified with knowing that $ \phi $ have a provision significance similar to that of knowing that $ \phi $ . To go through, my challenge thus requires the second of the following two views. On the first, knowing that $ \phi $ resembles hitting the bull’s eye, being 180 centimetres tall, and earning at least 9000€ insofar as its provision significance is due to the fact that our epistemic community has, in some implicit way, stipulated that knowing that $ \phi $ has that provision significance. On the second view, knowing that $ \phi $ instead resembles pain and friendship insofar as some provision significance it possesses is wholly due to what the property of knowing that $ \phi $ is. ¹²

The second view strikes me as more plausible; but defending it is a task I cannot take up here. So for present purposes, I’ll leave my conclusion in conditional form: if knowing that $ \phi $ resembles pain and friendship, rather than hitting the bull’s eye, being at least 180 centimetres tall, and earning at least 9000€, then we have reason to reject reductive views of knowing that $ \phi $ that appeal to a gradable property. Despite its conditional form, my conclusion is significant: it’s a substantive discovery that the plausibility of a wide range of reductive views of knowing that $ \phi $ turns on what knowing that $ \phi $ ’s provision significance is due to.

5. The challenge

Let’s put the pieces we’ve assembled in the last three sections together to mount my challenge. Focus on the reductive view according to which knowing that $ \phi $ at w just is safely believing that $ \phi $ at w. If knowing that $ \phi $ resembles pain and friendship, the small difference principle is inconsistent with this view.

To see this, recall that safely believing that $ \phi $ at w is identified with truly believing that $ \phi $ throughout a certain region of modal space, namely throughout the region encompassing all/sufficiently many of the worlds closest to w at which one believes that $ \phi $ . Call this region K. Now turn to the provision significance of knowing that $ \phi $ encoded in 5 and 8, and consider a jury who knows that the defendant is guilty (g). Given that knowing g is identical with truly believing g throughout K, and given (higher-order) Leibniz’s law, the fact that knowing g has provision significance entails that truly believing g throughout K has it, too. Truly believing g throughout K is necessary and sufficient for the jury to have an obligation to convict; and it immediately grounds this obligation.

Suppose now that the jury truly believes g throughout the region of modal space we obtain by removing a single world at K’s border from K. Call this region of modal space $ K-1 $ . Truly believing g throughout $ K-1 $ is not provision significant in anything like the way that knowing g is. It is neither necessary nor sufficient for the jury to have an obligation to convict; nor does it immediately ground the jury’s obligation (the jury doesn’t even have one).

However, the property of truly believing g throughout K is intrinsically very similar to the property of truly believing g throughout $ K-1 $ . On our ordering by size of region of modal space, they are almost exactly on a par, and there’s no other intrinsic difference between them. Yet on our reductive view, the first—identified with knowing g—has the provision significance encoded in 5 and 8, whilst the second does not. Since the property of truly believing g throughout $ K-1 $ also doesn’t have any provision significance distinct from, but similar to that encoded in 5 and 8, the two don’t have a similar provision significance. Assuming that knowing that $ \phi $ resembles pain and friendship, rather than hitting the bull’s eye, being at least 180 centimetres tall, and earning at least 9000€, this violates the small difference principle. Our reductive view predicts a normative discontinuity not licensed by the small difference principle. Thus, we have reason to reject the targeted reductive view.

In reply, we may question my application of (higher-order) Leibniz’s law on the ground that applications of Leibniz’s law are illegitimate in some contexts. To illustrate, suppose property F reduces to property G, albeit in an informative way: the discovery of this reduction was a significant achievement. (An example might be being water and being a sufficiently large, sufficiently pure agglomeration of H₂O molecules.) Before that achievement was had and we found out that F reduces to G, we may have thought that F was in need of reduction, but not G. In which case F and G had different properties: we thought that F was in need of reduction, but not G. This, however, does not undermine the reduction we eventually accomplished. Instead, use of the predicate ‘think that $ \phi $ ’ creates a context in which application of Leibniz’s law is illegitimate: thus, we cannot conclude from our thinking that F was in need of reduction, that we thought that G was in need of reduction.

The only predicate that could be the source of a similar effect in the transition from the claim that knowing g has provision significance to the claim that truly believing g throughout K has provision significance is the predicate ‘has provision significance.’ Is there any reason to think that it behaves the way ‘think that $ \phi $ ’ does? To answer this question, we need to unpack what is meant by provision significance. As Pautz and I understand it, to have such a significance is, primarily, to immediately ground a certain normative status. ¹³ For instance, pain-16’s provision significance is, primarily, its immediately grounding a pro tanto reason of a certain strength to want it to stop; similarly, the provision significance of the jury’s knowing g encoded in 5 and 8 is, primarily, its immediately grounding the jury’s obligation to convict.

The question whether the predicate ‘has provision significance’ behaves the way ‘think that $ \phi $ ’ does thus becomes the question whether grounding claims create contexts in which application of (higher-order) Leibniz’s law is illegitimate. However, insofar as grounding is taken to be a metaphysical dependence relation (rather than a conceptual dependence relation), grounding claims behave quite unlike ‘think that $ \phi $ ’: they don’t express a mental property with a representational “aspect.” At first glance, then, grounding claims don’t appear to create contexts in which applying (higher-order) Leibniz’s law is illegitimate.

Moreover, if the identity of two properties is sufficient for them to play the same role in grounding, as is commonly assumed (Audi 2016, 2012), we don’t even need to apply Leibniz’s law. For given this, if the jury’s knowing g immediately grounds its obligation to convict and knowing g is identical to believing g throughout K, as the reductive view claims, then the jury’s believing g throughout K immediately grounds its obligation to convict, too. Thus, we still predict a normative discontinuity between the jury’s believing believing g throughout K and its believing g throughout $ K-1 $ .

An alternative reply insists that I have only shown that truly believing g throughout K and throughout $ K-1 $ don’t have the same normative significance, but not that they don’t have a similar normative significance. Of course, truly believing g throughout $ K-1 $ neither suffices for, nor immediately grounds, the jury’s obligation to convict. But it does suffice for, and immediately grounds, its nearly having this obligation. Moreover, in this case, the jury comes closer to having this obligation than it would if it truly believed g throughout $ K-2 $ (a region of modal space missing two worlds at the border of K), $ K-3 $ , and so on. And the provision significance of truly believing g throughout $ K-1 $ and throughout $ K-2 $ respectively, as well as of truly believing g throughout $ K-2 $ and $ K-3 $ respectively, is similar. But then, the reply goes, if nearly having the obligation to convict (in the $ K-1 $ case) and not-quite-so-nearly having it (in the $ K-2 $ case) are similar normative statuses, why shouldn’t having it (in the K case) and nearly having it (in the $ K-1 $ case) be similar normative statuses? Thus, shouldn’t we regard truly believing g throughout K and throughout $ K-1 $ respectively as having a similar provision significance? If so, we register no violation of the small difference principle.

Pace the reply, however, we should not regard having the obligation and nearly having the obligation as similar normative statuses, despite the fact that nearly having it and not-quite-so-nearly having it are. For one, unlike having an obligation, nearly having an obligation is a modal property, something like the property of its being an easy possibility to have the target obligation. For another, having an obligation significantly differs normatively from not having that obligation, even if two ways of not having that obligation (nearly and not-quite-so-nearly) don’t. For instance, the jury’s having the obligation entitles others to reprimand it if it doesn’t convict; if the jury didn’t have the obligation, however, even if it nearly had the obligation, others wouldn’t have this entitlement.

The argument in this section aimed to show that conditional on knowing that $ \phi $ resembling pain and friendship insofar as (at least some of) its provision significance is wholly due to what knowing that $ \phi $ is, the targeted reductive view of knowing that $ \phi $ is inconsistent with the small difference principle. This conclusion can easily be shown to generalise to any reductive view that uses a gradable property, such as the four further views sketched in section 2. Absent independent evidence against the small difference principle, and if knowing that $ \phi $ resembles pain and friendship, rather than hitting the bull’s eye, being 180 centimetres tall, and earning at least 9000€, I suggest we reject reductive views of knowing that $ \phi $ that appeal to a gradable property. ¹⁴

6. Concluding remarks

My aim here has been to develop a challenge to reductive views of knowledge that appeal to a gradable property. My argument has been conditional on two assumptions that I take to be plausible, but haven’t defended here. The first assumption was that knowing that $ \phi $ has some provision significance, i.e., is a necessary and sufficient condition for, and immediately grounds, a normative status; the second that some provision significance of knowing that $ \phi $ is wholly due to what knowing that $ \phi $ is. This leaves defenders of reductive views that appeal to a gradable property with two escape routes. They can reject either the first or the second assumption. Rejecting the first, they would say that knowing that $ \phi $ doesn’t have any provision significance, for instance by denying that it is a necessary and sufficient condition for any normative status or by holding that any normative status it is necessary and sufficient for immediately grounds knowing that $ \phi $ instead of the other way around. Rejecting the second assumption, they would claim that whatever provision significance knowing that $ \phi $ does have is due to an implicit stipulation by the epistemic community.

By denying either of my two assumptions, however, defenders of reductive views that appeal to a gradable property take onboard substantive commitments. So, despite the fact that they have two escape routes left, the results of my discussion are significant. My argument shows that the plausibility of a wide range of reductive views of knowing that $ \phi $ depends on substantive commitments regarding whether knowing that $ \phi $ has a normative significance and, if so, what that significance is due to. Anyone inclined toward rejecting these commitments and accepting my two assumptions—such as myself—has reason to abandon reductive views of knowledge that appeal to a gradable property.

If we do abandon reductive views that appeal to a gradable property, where does this leave us? One way to retreat is to attempt to reduce knowing that $ \phi $ without appeal to a gradable property. However, it’s unclear whether there are any plausible reduction bases of the required sort. ¹⁵ An alternative, more promising way to retreat is to abandon the reductive project altogether. Pautz’s (2017) discussion of the consequences of the small difference principle for reductive physicalism about consciousness suggests a view that avoids my challenge. On this view, knowing that $ \phi $ is immediately grounded in, rather than identical to, one of the reduction bases in section 2; thus, we might say, for instance, that knowing that $ \phi $ is immediately grounded in safely believing that $ \phi $ .

Two facts allow this view to avoid my challenge. To begin with, the fact that x’s being F immediately grounds x’s being G doesn’t entail that F and G are intrinsically alike. On the grounding view, by contrast with the reductive view, knowing that $ \phi $ is an addition to our ontology and so might differ significantly from other entities already included in it (although it might still, so-to-speak, be an “ontological free lunch” [Armstrong 1989, 56]). So, the grounding view doesn’t entail that knowing that $ \phi $ and safely believing that $ \phi $ are intrinsically alike. Hence, defenders of that view can, unlike defenders of the reductive view, say that knowing that $ \phi $ is intrinsically very different from truly believing that $ \phi $ throughout $ K-1 $ , despite the fact that truly believing that $ \phi $ throughout K and truly believing that $ \phi $ throughout $ K-1 $ are intrinsically very similar.

What’s the second fact that allows the grounding view to avoid my challenge? Recall that I formulated provision significance in terms of immediate grounding: the provision significance of the jury’s knowing g encoded in 5 and 8, for instance, consists primarily in the fact that knowing g immediately grounds the jury’s obligation to convict. But whilst, on the grounding view, truly believing g throughout K immediately grounds knowing g, it doesn’t immediately ground the jury’s obligation: it only grounds it mediately. Thus, truly believing g throughout K doesn’t have the provision significance of knowing g. For this reason, the fact that truly believing g throughout $ K-1 $ doesn’t have that provision significance either doesn’t trigger violations of the small difference principle, although truly believing g throughout K is intrinsically very similar to truly believing g throughout $ K-1 $ .