Denote by S and M respectively the complex vector spaces of simple and measurable complex valued functions defined on the finite measure space X. Let T be a positive linear map from S to M such that for each p, 1 < p < ∞, sup {||T f||p: f ∈ S, ||f||P ≦ 1} is finit. finite. T then has an extension to a bounded transformation of every LP(X), 1 < p < ∞ , and these extensions are "consistent". The norm of T as a transformation of Lp is denoted ||T||P. The aim of this note is to prove the following theorem.

This paper concerns relative complexity of an algebraic theory T and its affine part A, primarily for theories TR of modules over a ring R. TR, AR and R itself are all, or none, finitely generated or finitely related. The minimum number of relations is the same for TR and AR. The minimum number of generators is a very crude invariant for these theories, being 1 for AR if it is finite, and 2 for TR if it is finite (and 1 ≠ 0 in R). The minimum arity of generators is barely less crude: 2 for TR} and 2 or 3 for AR (1 ≠ 0). AR is generated by binary operations if and only if R admits no homomorphism onto Z2.

The stable homeomorphism conjecture in dimension n,SHC (n), says that every orientation preserving homeomorphism of Sn is stable, i.e. can be written as the composition of homeomorphisms, each of which are the identity on some open set. This is equivalent to the homeomorphism being isotopic to the identity [6]. Call a homeomorphism k-stable if it is isotopic to a homeomorphism which is the identity on Sk ⊂ Sn.

The relationship between compact and countably compact topological spaces has been studied by many topologists. In particular an important question is: “What conditions will make a countably compact space compact?” Conditions which are “covering axioms” have been extensively studied. The best results of this type appear in [19]. We wish to examine countably compact spaces which are separable or perfectly normal. Recall that a space is perfect if and only if every closed subset is a Gδ, and that a space is perfectly normal if and only if it is both perfect and normal. We show that the following statement follows from MA +┐ CH and thus is consistent with the usual axioms of set theory: Every countably compact perfectly normal space is compact. This result is Theorem 3 and can be understood without reading much of what goes before.

Most properties an algebraist needs in categories are reflected by regular functors, introduced in [6]. If is a regular and strongly finitary functor and has some nice properties, it can be shown that the left adjoint functor of G helps to characterize finitary and strongly finitary objects of . The property of being algebroidal can be lifted from to if a certain condition holds in . As an application, the implicational hull of subcategories can be constructed with the help of reduced products.

Suppose F is a topological vector space. Let ACm ≡ ACm[a, b] be the absolutely continuous m-dimensional vector valued functions y on the compact interval [a, b] with essentially bounded components. Consider the boundary value problem

(1.1) where A0, A are respectively... operator with range in F.

In this paper we investigate methods for estimating the dimension of the null space of operators in a finite W* algebra, the dimension being measured by the trace τ. For the most part we are concerned with operators A which are a finite linear combination of orthogonal unitaries. We give various results which show how certain information about the unitaries and the coefficients can be utilized to derive an upper bound for τ(NA) where NA is the null space of A.

Let X be an infinite topological space, let 𝔫 be an infinite cardinal number with 𝔫 ≦ |X|. The basic problem in this paper is to find the number of closed sets in X of cardinality 𝔫. A complete answer to this question for the class of metrizable spaces has been given by A. H. Stone in [31], where he proves the following result. Let X be an infinite metrizable space of weight 𝔪, let 𝔫 ≦ |X|.

The main result of this paper is the following:

THEOREM. Every finitely generated orthomodular lattice L with finitely manymaximal Boolean subalgebras (blocks) is finite.

If L has one block only, our theorem reduces to the well-known fact that every finitely generated Boolean algebra is finite. On the other hand, it is known that a finitely generated orthomodular lattice without any further restrictions can be infinite. In fact, in [2] we constructed an orthomodular lattice which is generated by a three-element set with two comparable elements, has infinitely many blocks and contains an infinite chain.

A conference matrix of order n is a square matrix C with zeros on the diagonal and ±1 elsewhere, which satisfies the orthogonality condition CCT = (n — 1)I. If in addition C is symmetric, C =CT, then its order n is congruent to 2 modulo 4 (see [5]). Symmetric conference matrices (C) are related to several important combinatorial configurations such as regular two-graphs, equiangular lines, Hadamard matrices and balanced incomplete block designs [1; 5; and 7, pp. 293-400]. We shall require several definitions.

It was in the year 1931 that Dieudonné [4] proved the following necessary and sufficient condition for a polynomial to be univalent in the unit disk.

THEOREM A (Dieudonné criterion). The polynomial

(1)

is univalent in |z| < 1 if and only if for every θ in [0, π/2] the associated polynomial

(2)

does not vanish in |z| < 1. For θ = 0, ϕ(z, θ) is to be interpreted as Pn'(z).

Let R be a ring with involution*. In this paper, we study additive subgroups A of R which are invariant under all mappings of the form ϕx : a → xax*. That is, xAx* ⊆ A for all x ∈ R. Obvious examples of such subgroups A are ideals of R, the set of symmetric elements, and the set of skew-symmetric elements. We will prove that when R is *-prime, these examples are essentially the only ones.

Dans ce travail, nous étudions l'approximation polynomiale pondérée usuelle et aussi unilatérale dans l'espace L. Le poids considéré est w(x) = exp (—|x|) ce qui constitue un cas extremal; rappelons à ce propos quelques résultats de G. Freud. A chaque poids de la forme wQ(x) = exp ( — (Q(#)) correspond une suite caractéristique {qn} de nombres positifs définis par la relation qnQ’ (qn) = n. Dans le sixième chapitre de [1] (voir aussi [14]), Freud démontre que toute fonction/ pour laquelle ƒwQ ∊ L peut être approchée par un polynôme pn de degré ≤n en commettant une erreur (∫|fƒ -Pn\wQ) d'au plus Ω(ƒ, qn/n) où Ω est un module de continuité adéquat et obtient des résultats précisés lorsque la fonction ƒ est supposée differentiate. Dans [2], Freud montre que si la r ième dérivée f(r) est à support compact et à variation bornée et si |ƒ| admet une majoration polynomiale, alors/ peut être approchée unilatéralement par des polynômes de degré ≦n (pn ≦ ƒ ≦ Pn) avec une erreur (∫(Pn — pn)wQ) inférieure à K(ƒ)(qn/n)r+1. Lorsque Q(x) = |x|p, on a qn ~ n1/p de telle sorte que, si ρ > 1, qn/n tend vers zéro avec \/n mais, si ρ = 1, le prolongement formel direct des résultats de Freud fournit une majoration de l'erreur ne tendant pas vers zéro avec 1/n. Cependant, il suit des recherches de M. Riesz [3] (voir aussi [4]) que les fonctions à croissance polynomiale peuvent être approchées unilatéralement dans l'espace L avec poids w et, en particulier, que les polynômes sont denses dans cet espace.

If a locally compact group G acts as a measure preserving transformation group on a Lebesgue space X, then there is a naturally induced unitary representation of G on L2(X), and one can study the action on X by means of this representation. The situation in which the representation has discrete spectrum (i.e., is the direct sum of finite dimensional representations) and the action is ergodic was examined by von Neumann and Halmos when G is the integers or the real line [7], and by Mackey for general non-abelian G [10].

For partially ordered sets X and F let Yx denote the set of all order-preserving maps of X to Y partially ordered by f ≦ g if and only if f(x)≦ g (x) for each x ∈ X [1; 4; 6]. If X is unordered then Yx is the usual direct product of partially ordered sets, while if both X and Y are finite unordered sets then Yx is the commonplace exponent of cardinal numbers. This generalized exponentiation has an important vindication especially for those partially ordered sets that are lattices.

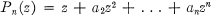
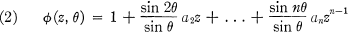
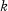The genesis of this paper is the following well known result in field theory: Let R denote a field of characteristic p ≠ 0, and let denote a subfield of 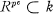R such that for some 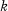e sufficiently large. Then R is isomorphic to the tensor product (over ) of primitive extensions of 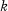if and only if there exists a finite set Γ of -higher derivations on R such that is the field of constants of Γ. A proof of this theorem can be found in [6].

Let Mn(C) be the vector space of all w-square complex matrices. Denote by (• , •) the standard inner product in the space Cn of complex n-tuples. For a matrix A ∈ Mn(C) and an n-tuple c = (c1,… , cn) ∈ Cn, define the c-numerical range of A to be the set

(1)

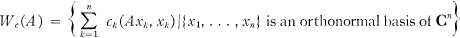
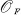Let F be a local field of characteristic zero, with q elements in its residue field, ring of integers uniformizer ω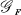F and maximal ideal . Let GF = GL2(F). We fix Haar measures dg and dz on GF and ZF, the centre of GF, so that

meas(K) = meas

where K = GL2() is a maximal compact subgroup of GF. If T is a torus in GF we take dt to be the Haar measure on T such that

means(TM)=1

where TM denotes the maximal compact subgroup of T.