Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-25T05:55:26.130Z Has data issue: false hasContentIssue false
  • English
  • Français

The Word Problem for Orthogroups

Published online by Cambridge University Press:  20 November 2018

J. A. Gerhard  and
Mario Petrich
J. A. Gerhard
Affiliation:
University of Manitoba, Winnipeg, Canada
Mario Petrich
Affiliation:
University of Manitoba, Winnipeg, Canada
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A semigroup which is a union of groups is said to be completely regular. If in addition the idempotents form a subsemigroup, the semigroup is said to be orthodox and is called an orthogroup. A completely regular semigroup S is provided in a natural way with a unary operation of inverse by letting a-l for a ∈ S be the group inverse of a in the maximal subgroup of S to which a belongs. This unary operation satisfies the identities

(1)

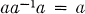
(2)

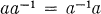
(3)

In fact a completely regular semigroup can be defined as a unary semigroup (a semigroup with an added unary operation) satisfying these identities. An orthogroup can be characterized as a completely regular semigroup satisfying the additional identity

(4)

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 33 , Issue 4 , 01 August 1981 , pp. 893 - 900
Copyright
Copyright © Canadian Mathematical Society 1981

References

1. Clifford, A. H., The free completely regular semigroup on a set, J. Algebra 59 (1979), 434–451.Google Scholar
2. Howie, J. M., An introduction to semigroup theory (Academic Press, London, 1976).Google Scholar
3. Liber, S. A., On free algebras of normal closures of varieties, Ordered Sets and Lattices, Issue 2, Saratov (1974), 51-53. (In Russian).Google Scholar
4. Petrich, M., Varieties of orthodox bands of groups, Pacific J. Math. 58 (1975), 209–217.Google Scholar
5. Yamada, M., Strictly inversive semigroups, Bull. Shimane Univ. 13 (1964), 128–138.Google Scholar