Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-24T16:02:34.334Z Has data issue: false hasContentIssue false
  • English
  • Français

Well Ramified Extensions of Complete Discrete Valuation Fields with Applications to the Kato Conductor

Published online by Cambridge University Press:  20 November 2018

Luca Spriano
Luca Spriano*
Affiliation:
Université Bordeaux I, 351, Cours de la Libération, 33405 Talence, France email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study extensions 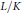$L/K$ of complete discrete valuation fields 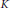$K$ with residue field 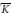$\bar{K}$ of characteristic 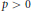$p\,>\,0$, which we do not assume to be perfect. Our work concerns ramification theory for such extensions, in particular we show that all classical properties which are true under the hypothesis “the residue field extension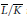$\bar{L}/\bar{K}$is separable” are still valid under the more general hypothesis that the valuation ring extension is monogenic. We also show that conversely, if classical ramification properties hold true for an extension 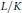$L/K$, then the extension of valuation rings is monogenic. These are the “well ramified” extensions. We show that there are only three possible types of well ramified extensions and we give examples. In the last part of the paper we consider, for the three types, Kato’s generalization of the conductor, which we show how to bound in certain cases.

Keywords

11S11S1511S20
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 52 , Issue 6 , 01 December 2000 , pp. 1269 - 1309
Copyright
Copyright © Canadian Mathematical Society 2000

References

[B-C-S] Boltje, R., Martin Cram, G. and Snaith, V. P., Conductors in the non-separable residue field case. Algebraic K-Theory and Algebraic Topology, Kluwer Acad. Publ., 1993, 1–34.Google Scholar
[BDS1] de Smit, B., The different and differentials of local fields with imperfect residue field. Proc. Edinburgh Math. Soc. 40(1997), 353–365.Google Scholar
[BDS2] de Smit, B., Ramification groups of local fields with imperfect residue class field. J. Number Theory (3) 44(1993), 229–236.Google Scholar
[B] Borger, J., A monogenic Hasse-Arf theorem. Proceedings of the Conference on Ramification theory for arithmetic schemes, Luminy, 1999, to appear.Google Scholar
[E] Epp, H. P., Eliminating wild ramification. Invent. Math. 19(1973), 235–249.Google Scholar
[F-V] Fesenko, I. and Vostokov, V., Local fields and their extensions. Trans. Math. Monographs, Amer. Math. Soc., 1993.Google Scholar
[Her] Herbrand, M. J., Sur la théorie des groupes de décomposition, d’inertie et de ramification. J. de Liouville, 1931.Google Scholar
[H] Hyodo, O., Wild ramification in the imperfect residue field case. Galois Representations and Arithmetic Algebraic Geometry, Adv. Stud. Pure Math. 12(1987), 287–314.Google Scholar
[K1] Kato, K., A generalization of local class field theory by using K-groups I. J. Fac. Sci. Univ. Tokyo, Sect. IA 26(1979), 303–376; II, ibid., 27 (1980), 603–683.Google Scholar
[K2] Kato, K., Swan conductors with differential values. Adv. Stud. Pure Math. 12(1987), 315–342.Google Scholar
[K3] Kato, K., Swan conductors for characters of degree one in the imperfect residue field case. Contemp. Math. 83(1989), 101–131.Google Scholar
[K4] Kato, K., Vanishing cycles, ramification of valuations, and class field theory. Duke Math. J. (3) 55(1987), 629–659.Google Scholar
[Ku] Kurihara, M., On two types of discrete valuation fields. Compositio Math. 63(1987), 237–257.Google Scholar
[M-W] MacKenzie, R. E. and Whaples, G., Artin-Schreier equations in characteristic zero. Amer. J. Math. 78(1956), 473–485.Google Scholar
[M] Miki, H., On zp-extensions of complete p-adic power series fields and function fields. J. Fac. Sci. Univ. Tokyo Sect. IA 21(1974), 377–393.Google Scholar
[P] Paršin, A. N., Abelian coverings of arithmetic schemes. Soviet Math. Dokl. 19(1978), 1438–1442.Google Scholar
[Po] Poitou, G., Cohomologie Galoisienne des modules finis. Sém. Inst. Math. Lille DUNOD, Paris, 1967.Google Scholar
[Sen] Sen, S., On automorphisms of local fields. Ann. of Math. 90(1969), 33–46.Google Scholar
[S1] Serre, J.-P., Corps Locaux. 3rd edition, Hermann, Paris, 1967.Google Scholar
[S2] Serre, J.-P., Représentations linéaires des groupes finis. Hermann, Paris, 1967.Google Scholar
[S3] Serre, J.-P., Sur la rationalité des représentations d’Artin. Ann. of Math. 72(1960), 406–420.Google Scholar
[Sn] Snaith, V. P., Explicit Brauer induction. Cambridge University Press, 1994.Google Scholar
[Sp] Spriano, L., Well and fiercely ramified extensions of complete discrete valuation fields with application to the Kato conductor. Université de Bordeaux 1, 1999.Google Scholar
[Wi] Williamson, S., Ramification theory for extensions of degree p. NagoyaMath. J. 41(1971), 149–168.Google Scholar
[Wy] Wyman, B., Wildly ramified gamma extensions. Amer. J. Math. 91(1969), 135–152.Google Scholar
[Z-S] Zariski, O. and Samuel, P., Commutative algebra, Vol. I. Graduate Texts in Math. 28, Springer, 1960.Google Scholar
[Zh] Zhukov, I. B., On ramification theory in the imperfect residue field case. Preprint, University of Nottingham. 1998.Google Scholar