Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-26T16:26:34.077Z Has data issue: false hasContentIssue false
  • English
  • Français

Weak Mixing Manifold Homeomorphisms Preserving an Infinite Measure

Published online by Cambridge University Press:  20 November 2018

Steve Alpern  and
Vidhu Prasad
Steve Alpern
Affiliation:
London School of Economics, London, England
Vidhu Prasad
Affiliation:
York University, North York, Ontario
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 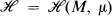denote the group of all homeomorphisms of a σ-compact manifold which preserve a σ-finite, nonatomic, locally positive and locally finite measure μ. In two recent papers [4, 5] the possible ergodicity of a homeomorphism h in 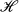was shown to be related to the homeomorphism h* induced by h on the ends of M. An end of a manifold is, roughly speaking, a distinct way of going to infinity. Those papers demonstrated in particular that 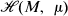always contains an ergodic homeomorphism, paralleling the similar result of Oxtoby and Ulam [11] for compact manifolds with finite measures. Unfortunately the techniques used in [4] and [5] rely on the fact that a skyscraper construction with an ergodic base transformation is ergodic, a result which cannot be extended to finer properties than ergodicity.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 39 , Issue 6 , 01 December 1987 , pp. 1475 - 1488
Copyright
Copyright © Canadian Mathematical Society 1987

References

1. Alpern, S., Return times and conjugates of an antiperiodic transformation, Erg. Th. and Dyn. Sys. 1 (1981), 135–143.Google Scholar
2. Alpern, S., Nonstable ergodic homeomorphisms of R , Indiana Univ. Math. J. 32 (1983), 187–191.Google Scholar
3. Alpern, S. and Edwards, R., Lusin's theorem for measure preserving homeomorphisms, Mathematika 26 (1979), 33–43.Google Scholar
4. Alpern, S. and Prasad, V., End behaviour and ergodicity for homeomorphisms of manifolds with finitely many ends, Can. J. Math. 39 (1987), 473–491.Google Scholar
5. Alpern, S. and Prasad, V., Dynamics induced on the ends of a noncompact manifold, Eng. Th. and Dyn. Sys. 7 (to appear).Google Scholar
6. Antoine, L., Sur Thoméomorphie de deux figures et de leurs voisinages, J. Math. Pures Appl. 4(1921), 221–325.Google Scholar
7. Berlanga, R. and Epstein, D., Measures on σ-compact manifolds and their equivalence under homeomorphisms, J. London Math. Soc. 27 (1983), 63–74.Google Scholar
8. Choksi, J. and Kakutani, S., Residuality of ergodic measurable transformations and of ergodic transformations which preserve an infinite measure, I6ndiana Univ. Math. J. 28 (1979), 453–469.Google Scholar
9. Keldys, L., Topological embeddings in Euclidean space, Proc. Steklov Inst. Math. 81 (1966) (Translation, Amer. Math. Soc., 1968).Google Scholar
10. Oxtoby, J., Approximation by measure preserving homeomorphisms, Recent Advances in Topological Dynamics, Springer Lecture Notes in Math. 318 (1973), 206–217.Google Scholar
11. Oxtoby, J. and Ulam, S., Measure preserving homeomorphisms and metrical transitivity, Ann. of Math. 42 (1941), 874–920.Google Scholar
12. Sachdeva, U., On the category of mixing in infinite measure spaces, Math. Systems Th. 5 (1971), 319–330.Google Scholar
13. White, H. E. Jr., The approximation of one-one measurable transformations by measure preserving homeomorphisms, Proc. Amer. Math. Soc. 44 (1974), 391–394.Google Scholar