Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-20T12:31:36.119Z Has data issue: false hasContentIssue false
  • English
  • Français

The Weak b-principle: Mumford Conjecture

Published online by Cambridge University Press:  20 November 2018

Rustam Sadykov
Rustam Sadykov*
Affiliation:
Department of Mathematics, CINVESTAV, Av. Instituto Politecnico Nacional 2508, Col. San Pedro Zacatenco, Mexico, D.F. CP 07360 e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this note we introduce and study a new class of maps called oriented colored broken submersions. This is the simplest class of maps that satisfies a version of the 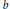$b$–principle and in dimension 2 approximates the class of oriented submersions well in the sense that every oriented colored broken submersion of dimension 2 to a closed simply connected manifold is bordant to a submersion. We show that the Madsen–Weiss theorem (the standard Mumford Conjecture) fits a general setting of the 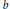$b$–principle, namely, a version of the 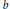$b$–principle for oriented colored broken submersions together with the Harer stability theorem and Miller–Morita theorem implies the Madsen–Weiss theorem.

Keywords

55N2053C23generalized cohomology theoriesfold singularitiesh-principleinfinite loop spaces
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 68 , Issue 2 , 01 April 2016 , pp. 463 - 480
Copyright
Copyright © Canadian Mathematical Society 2016

References

[1] Ando, Y., Cobordisms of maps with singularities of a given class. Algebr. Geom. Topol. 8(2008), 1989–2029.http://dx.doi.org/10.2140/agt.2008.8.1989 Google Scholar
[2] Audin, M., Cobordismes d'immersions lagrangiennes et legendriennes. Thèse d'état (Orsay, 1986), Travaux en Cours, Hermann, Paris, 1987.Google Scholar
[3] Barratt, M. and Priddy, P., On the homology of non-connected monoids and their associated groups. Comment. Math. Helv. 47(1972), 1–14.http://dx.doi.org/10.1007/BF02566785 Google Scholar
[4] Eliashberg, Y., Galatius, S., and Mishachev, N., Madsen–Weiss for geometrically minded topologists. Geom. Topol. 15(2011), 411–472.http://dx.doi.org/10.2140/gt.2011.15.411 Google Scholar
[5] Eliashberg, Y., Cobordisme des solutions de relations différentielles. In: South Rhone seminar on geometry I (Lyon, 1983), Travaux en Cours, Hermann, Paris, 1984, 17–31.Google Scholar
[6] Eliashberg, Y. and Mishachev, N., Introduction to the h-principle. Grad. Stud. Math. 48, Amer. Math. Soc., Providence, Rhode Island, 2002.Google Scholar
[7] Galatius, S., Madsen, I., Tillmann, U., and Weiss, M., The homotopy type of the cobordism category. Acta Math. 202(2009), 195–239. http://dx.doi.org/10.1007/s11511-009-0036-9 Google Scholar
[8] Galatius, S. and Randal-Williams, O., Monoids of moduli spaces of manifolds. Geom. Topol. 14(2010),1243–1302. http://dx.doi.org/10.2140/gt.2010.14.1243 Google Scholar
[9] Gromov, M., Partial differential relations. Springer-Verlag, Berlin, Heidelberg, 1986.Google Scholar
[10] Hatcher, A., A short exposition of the Madsen–Weiss theorem.Preprint.Google Scholar
[11] Madsen, I. and Weiss, M. S., The stable moduli space of Riemann surfaces: Mumford's conjecture. Ann. of Math. (2) 165(2007), 843–941.http://dx.doi.org/10.4007/annals.2007.165.843 Google Scholar
[12] Morita, Sh., Geometry of characteristic classes. Transl. Math. Monogr. 199, Amer. Math. Soc., Providence, RI, 2001.Google Scholar
[13] Rimányi, R. and Szűcs, A., Pontrjagin–Thom type construction for maps with singularities. Topology 37(1998), 1177–1191.http://dx.doi.org/10.1016/S0040-9383(97)00093-1 Google Scholar
[14] Sadykov, R., The bordism version of the h-principle. Preprint.Google Scholar
[15] Sadykov, R., The weak b-principle. Contemp. Math. 621(2014), 101–112.Google Scholar
[16] Sadykov, R., Bordism groups of special generic mappings. Proc. Amer. Math. Soc. 133(2005), 931–936.http://dx.doi.org/10.1090/S0002-9939-04-07586-0 Google Scholar
[17] Sadykov, R., Bordism groups of solutions to differential relations. Algebr. Geom. Topol. 9(2009), 2311–2349.http://dx.doi.org/10.2140/agt.2009.9.2311 Google Scholar
[18] Schlichtkrull, Ch., Units of the ring spectra and their traces in algebraic K-theory. Geom. Topol. 8(2004), 645–673.http://dx.doi.org/10.2140/gt.2004.8.645 Google Scholar
[19] Szűcs, A., Cobordism of singular maps. Geom. Topol. 12(2008), 2379–2452.http://dx.doi.org/10.2140/gt.2008.12.2379 Google Scholar
[20] Wells, R., Cobordism groups of immersions. Topology 5(1966), 281–294.http://dx.doi.org/10.1016/0040-9383(66)90011-5 Google Scholar