No CrossRef data available.
Article contents
Wallman Compactification and Representation
Published online by Cambridge University Press: 20 November 2018
Extract
Let X be any set and A be a uniformly closed algebra of bounded real valued functions on X which contains the constants and separates the points. For a lattice ℒ of subsets of X (we assume throughout that ∅ and X belong to ℒ), let MR(ℒ) denote the space of all finite, finitely additive,ℒ-regular measures defined on the field of sets generated by ℒ . Generalizing the notion of an integral representation, in [5] Kirk and Crenshaw define a standard representation of A*, the Banach dual of A, in MR(ℒ) to be a linear map I of A* into MR(ℒ) with the property that if 0 ≦ ϕ ∈ A*, then
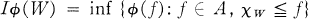
for every W in ℒ. The space MR(ℒ) is said to represent A* if there exists a (unique) standard representation I of A* onto MR(ℒ) which is a Banach lattice isomorphism.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1981


