Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-14T03:26:30.990Z Has data issue: false hasContentIssue false
  • English
  • Français

Variations of Mixed Hodge Structures of Multiple Polylogarithms

Published online by Cambridge University Press:  20 November 2018

Jianqiang Zhao
Jianqiang Zhao*
Affiliation:
Department of Mathematics, Eckerd College, St. Petersburg, FL 33711, U.S.A. e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

It is well known that multiple polylogarithms give rise to good unipotent variations of mixed Hodge-Tate structures. In this paper we shall explicitly determine these structures related to multiple logarithms and some other multiple polylogarithms of lower weights. The purpose of this explicit construction is to give some important applications. First we study the limit of mixed Hodge-Tate structures and make a conjecture relating the variations of mixed Hodge-Tate structures of multiple logarithms to those of general multiple polylogarithms. Then following Deligne and Beilinson we describe an approach to defining the single-valued real analytic version of the multiple polylogarithms which generalizes the well-known result of Zagier on classical polylogarithms. In the process we find some interesting identities relating single-valued multiple polylogarithms of the same weight $K$ when 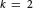$K=2$ and 3. At the end of this paper, motivated by Zagier's conjecture we pose a problem which relates the special values of multiple Dedekind zeta functions of a number field to the single-valued version of multiple polylogarithms.

Keywords

14D0714D0533B30
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 56 , Issue 6 , 01 December 2004 , pp. 1308 - 1338
Copyright
Copyright © Canadian Mathematical Society 2004

References

[1] Beilinson, A.A. and Deligne, P., Interprétation motivique de la conjecture de Zagier reliant polylogarithmes et régulateurs. In: Motives, Proc. Sym. Pure Math., 55, Amer.Math. Soc., Providence, RI, 1994, pp. 97–121.Google Scholar
[2] Beilinson, A.A., Goncharov, A.B., Schechtman, V.V. and Varchenko, A.N., Aomoto dilogarithms, mixed Hodge structures and motivic cohomology of pairs of triangles on the plane. In: Grothendieck Festschrift I, Prog. in Math., 87 Birkhäuser, Boston, 1991, pp. 155–172.Google Scholar
[3] Bloch, S., Lectures on mixed motives given at Santa Cruz, 1995, available online http://www.math.uchicago.edu/bloch/publications.html.Google Scholar
[4] -Chen, K.-T., Algebras of iterated path integrals and fundamental groups. Trans. Amer. Math. Soc. 156(1971), 359–379.Google Scholar
[5] Deligne, P., Letter to Spencer Bloch, April 3, 1984.Google Scholar
[6] Deligne, P., Equations differentielles ´a points singuliers réguliers. Lecture Notes in Math., 163, Springer-Verlag, Berlin, 1970.Google Scholar
[7] Deligne, P. and Goncharov, A., Groupes fondamentaux motiviques de Tate mixte. http://arxiv.org/abs/math.NT/0302267.Google Scholar
[8] Goncharov, A.B.,Polylogarithms in arithmetic and geometry. In: Proc. Internatonal Congress of Mathematicians I, Birkhäuser, 1994. pp. 374–387.Google Scholar
[9] Goncharov, A.B., The double logarithm and Manin's complex for modular curves. Math. Res. Letters 4(1997), 617–636.Google Scholar
[10] Hain, R., Classical polylogarithms. In: Motives, Proc. Sym. Pure Math., 55, Amer.Math. Soc., Providence, RI, 1994, pp. 3–42.Google Scholar
[11] Hain, R. and MacPherson, R., Higher logarithms. Illinoia J. Math. 34(1990), 392–475.Google Scholar
[12] Hain, R. and Zucker, S., Unipotent variations of mixed Hodge structure. Invent.Math. 88(1987), 83–124.Google Scholar
[13] Hain, R. and Zucker, S., A guide to unipotent variations of mixed Hodge structure. In: Hodge Theory, Lecture Notes in Math., 1246, Springer, Berlin, 1987, pp. 92–106 Google Scholar
[14] Poincaré, H., Oeuvres, vol. 2, Gauthier-Vilars, Paris, 1916.Google Scholar
[15] Steenbrink, J. and Zucker, S., Variation of mixed Hodge structure. I. InventMath. 80(1985), 489–542.Google Scholar
[16] Wojtkowiak, Z., Mixed Hodge structures and iterated integrals. I. In: Motives, polylogarithms and Hodge theory, Int. Press Lect. Ser, 3, Int. Press, Somerville, MA, 2002, pp. 121–208.Google Scholar
[17] Zagier, D., The Block-Wigner-Ramakrishnan polylogarithm function. Math. Ann. 286(1990), 613–624.Google Scholar
[18] Zhao, J., Motivic complexes of weight three and pairs of simplices in projective 3-space. Adv. Math. 161(2001), 141–208.Google Scholar
[19] Zhao, J., Multiple polylogarithms: analytic continuation, monodromy, and variations of mixed Hodge structures. In: Contemporary Trends in Algebraic Geometry and Algebraic Topology, (eds. Chern, S.S., Fu, L. and Hain, R.) Nankai Tracts Math., 5, World Scientific, 2002, pp. 167–193.Google Scholar