Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-24T10:52:06.976Z Has data issue: false hasContentIssue false
  • English
  • Français

Variations of Integrals in Diffeology

Published online by Cambridge University Press:  20 November 2018

Patrick Iglesias-Zemmour
Patrick Iglesias-Zemmour*
Affiliation:
LATP-CNRS, 39 rue F. Joliot-Curie, 13453 Marseille Cedex 13, France, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We establish a formula for the variation of integrals of differential forms on cubic chains in the context of diffeological spaces. Then we establish the diffeological version of Stokes’ theorem, and we apply that to get the diffeological variant of the Cartan–Lie formula. Still in the context of Cartan–De Rham calculus in diffeology, we construct a chain-homotopy operator 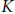$K$, and we apply it here to get the homotopic invariance of De Rham cohomology for diffeological spaces. This is the chain-homotopy operator that is used in symplectic diffeology to construct the moment map.

Keywords

58A1058A1258A40diffeologydifferential geometryCartan–De Rham calculus
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 65 , Issue 6 , 01 December 2013 , pp. 1255 - 1286
Copyright
Copyright © Canadian Mathematical Society 2013

References

[Che77] Chen, K. T., Iterated path integrals. Bull. of Am. Math. Soc. 83(1977), no. 5, 831–879. http://dx.doi.org/10.1090/S0002-9904-1977-14320-6 Google Scholar
[Don84] Donato, P., Revêtement et groupe fondamental des espaces différentiels homogènes. Doctorate dissertation, Université de Provence, Marseille, 1984.Google Scholar
[Don94] Donato, P., Diff(S1) as coadjoint orbit in the Virasoro space of moments. J. Geom. Phys. 13(1994), 299–305. http://dx.doi.org/10.1016/0393-0440(94)90037-X Google Scholar
[DI85] Donato, P. and Iglesias, P., Exemple de groupes difféologiques : flots irrationnels sur le tore. C. R. Acad. Sci. Paris Sér. I Math. 301(1985), no. 4, 127–130.Google Scholar
[Igl85] Iglesias, P., Fibrés difféologiques et homotopie. Doctorate dissertation, Université de Provence, Marseille, 1985.Google Scholar
[Piz05] Iglesias-Zemmour, P., Diffeology.eprint, 2005 – 2009. http://math.huji.ac.il/_piz/diffeology/. Google Scholar
[Piz06-b] Iglesias-Zemmour, P., Diffeology of the infinite Hopf fibration. In: Geometry and Topology of Manifolds, Banach Center Publ., 76, Polish Acad. Sci. Inst. Math.,Warszawa, 2007, pp. 349–393.Google Scholar
[Piz07] Iglesias-Zemmour, P., The moment maps in diffeology. Mem. Amer. Math. Soc. 207(2010), no. 972.Google Scholar
[Sou81] Souriau, J.-M., Groupes différentiels. In: Differential geometrical methods in mathematical physics (Proc. Conf., Aix-en-Provence/Salamanca, 1979), Lecture Notes in Mathematics, 836, Springer Verlag, New-York, 1981, pp. 91–128.Google Scholar
[Sou84] Iglesias-Zemmour, P., Groupes différentiels et physique mathématique. In: South Rhone seminar on geometry. II. (Lyons, 1983), Travaux en Cours, Hermann, Paris, 1984, pp. 73–119.Google Scholar