Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-25T06:14:03.880Z Has data issue: false hasContentIssue false
  • English
  • Français

Variational Methods for One and Several Parameter Non-Linear Eigenvalue Problems

Published online by Cambridge University Press:  20 November 2018

Paul Binding
Paul Binding*
Affiliation:
University of Calgary, Calgary, Alberta
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We shall consider a multiparameter eigenvalue problem of the form

(1.1)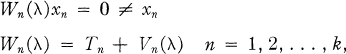

where λ ∈ Rk while Tn and Vn(λ) are self-adjoint linear operators on a Hilbert space Hn. If λ = (λ1, …, λk) ∈ Rk and 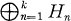satisfy (1.1) then we call λ an eigenvalue, x an eigenvector and (λ, x) an eigenpair. While our main thrust is towTards the general case of several parameters λn, the method ultimately involves reduction to a sequence of one parameter problems. Our chief contributions are (i) to generalise the conditions under which this reduction is possible, and (ii) to develop methods for the one parameter problem particularly suited to the multiparameter application. For example, we give rather general results on the magnitude and direction of the movement of non-linear eigenvalues under perturbation.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 33 , Issue 1 , 01 February 1981 , pp. 210 - 228
Copyright
Copyright © Canadian Mathematical Society 1981

References

1. Berger, M., Nonlinearity and functional analysis (Academic Press, 1977).Google Scholar
2. Binding, P., On the use of degree theory for non-linear multiparameter eigenvalue problems, J. Math. Anal. Appl. 73 (1980), 381–391.Google Scholar
3. Binding, P. and Browne, P. J., A variational approach to multiparameter eigenvalue problems in Hilbert space, SIAM J. Math. Anal. 9 (1978), 1054–1067.Google Scholar
4. Binding, P. and Browne, P. J., A variational approach to multiparameter eigenvalue problems for differential equations (to appear).Google Scholar
5. Böcher, M., The theorems of oscillation of Sturm and Klein 1, Bull. Amer. Math. Soc. 4 (1898), 295–313.Google Scholar
6. Böcher, M., The theorems of oscillation of Sturm and Klein 2, Bull. Amer. Math. Soc. 4 (1898), 365–376.Google Scholar
7. Browne, P., A completeness theorem for a non-linear multiparameter eigenvalue problem, J. Differential Equations, 23 (1977), 285–292.Google Scholar
8. Browne, P. and Sleeman, B., Nonlinear multiparameter Sturm-Liouville problems (to appear).Google Scholar
9. Estabrooks, M. and Macki, J., A nonlinear Sturm-Liouville problem, J. Differential Equations 10 (1971), 181–187.Google Scholar
10. Ince, E., Ordinary differential equations (Dover, 1944).Google Scholar
11. Klein, F., Über Lamésche Funktionen, Math. Ann. 18 (1881), 237–246.Google Scholar
12. Sleeman, B., The two parameter Sturm-Liouville problem for ordinary differential equations, Proc. Roy. Soc. Edin. A69 (1971), 139–148.Google Scholar
13. Sleeman, B., The two parameter Sturm-Liouville problem for ordinary differential equations II, Proc. Amer. Math. Soc. 34 (1972), 165–170.Google Scholar
14. Sleeman, B., Multiparameter spectral theory in Hilbert space, J. Math. Anal. Appl. 65 (1978), 511–530.Google Scholar
15. Tal, A., Eigenfunctions for a class of non-linear differential equations. J. Differential Equations, 3 (1967), 112–134.Google Scholar
16. Turner, R., Some variational principles for a non-linear eigenvalue problem, J. Math. Anal. Appl. 17 (1967), 151–160.Google Scholar
17. Turner, R., A class of nonlinear eigenvalue problems, J. Functional Anal. 2 (1968), 297–322.Google Scholar