No CrossRef data available.
Article contents
Universal Alternating Semiregular Polytopes
Published online by Cambridge University Press: 12 February 2020
Abstract
In the classical setting, a convex polytope is said to be semiregular if its facets are regular and its symmetry group is transitive on vertices. This paper continues our study of alternating semiregular abstract polytopes, which have abstract regular facets, still with combinatorial automorphism group transitive on vertices and with two kinds of regular facets occurring in an alternating fashion.
Our main concern here is the universal polytope 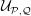 ${\mathcal{U}}_{{\mathcal{P}},{\mathcal{Q}}}$, an alternating semiregular
${\mathcal{U}}_{{\mathcal{P}},{\mathcal{Q}}}$, an alternating semiregular 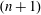 $(n+1)$-polytope defined for any pair of regular
$(n+1)$-polytope defined for any pair of regular  $n$-polytopes
$n$-polytopes 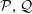 ${\mathcal{P}},{\mathcal{Q}}$ with isomorphic facets. After a careful look at the local structure of these objects, we develop the combinatorial machinery needed to explain how
${\mathcal{P}},{\mathcal{Q}}$ with isomorphic facets. After a careful look at the local structure of these objects, we develop the combinatorial machinery needed to explain how 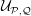 ${\mathcal{U}}_{{\mathcal{P}},{\mathcal{Q}}}$ can be constructed by “freely assembling” unlimited copies of
${\mathcal{U}}_{{\mathcal{P}},{\mathcal{Q}}}$ can be constructed by “freely assembling” unlimited copies of 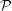 ${\mathcal{P}}$,
${\mathcal{P}}$, 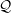 ${\mathcal{Q}}$ along their facets in alternating fashion. We then examine the connection group of
${\mathcal{Q}}$ along their facets in alternating fashion. We then examine the connection group of 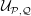 ${\mathcal{U}}_{{\mathcal{P}},{\mathcal{Q}}}$, and from that prove that
${\mathcal{U}}_{{\mathcal{P}},{\mathcal{Q}}}$, and from that prove that 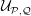 ${\mathcal{U}}_{{\mathcal{P}},{\mathcal{Q}}}$ covers any
${\mathcal{U}}_{{\mathcal{P}},{\mathcal{Q}}}$ covers any 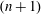 $(n+1)$-polytope
$(n+1)$-polytope 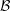 ${\mathcal{B}}$ whose facets alternate in any way between various quotients of
${\mathcal{B}}$ whose facets alternate in any way between various quotients of 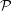 ${\mathcal{P}}$ or
${\mathcal{P}}$ or 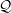 ${\mathcal{Q}}$.
${\mathcal{Q}}$.
MSC classification
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2020
Footnotes
The second author is supported by the Simons Foundation Award No. 420718.



