Hostname: page-component-745bb68f8f-kw2vx Total loading time: 0 Render date: 2025-01-12T11:22:08.007Z Has data issue: false hasContentIssue false
  • English
  • Français

Une Remarque Sur Une Classe D'Algebres De Dirichlet Faibles* De Fonctions Analytiques

Published online by Cambridge University Press:  20 November 2018

Michel Savoyant
Michel Savoyant*
Affiliation:
Université des Sciences et Techniques du Languedoc, Montpellier, Cédex, France
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Soit K un compact du plan complexe C, d'intérieur 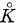non vide et connexe. A(K) désigne l'algèbre uniforme des fonctions continues sur 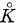et analytiques dans 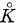. Pour chaque 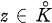, on note λz la mesure harmonique sur la frontièr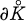e de 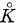du point z, et on pose λ = λz0, z0 étant un point fixé de 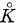. On dit que A(K) est une algèbre de Dirichlet faible* sur 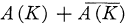(— désigne le conjugué) est faiblement* dense dans L∞(λ) (la topologie faible* sur L∞(λ) est la topologie faible pour la dualité entre L1(λ) et L∞(X)); vu les inégalités de Harnack pour les fonctions harmoniques cette propriété est indépendante de la mesure harmonique du point z0 fixé dans .

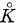Type
Research Article
Information
Canadian Journal of Mathematics , Volume 33 , Issue 6 , 01 December 1981 , pp. 1328 - 1330
Copyright
Copyright © Canadian Mathematical Society 1981

References

1. Davie, A. M., Bounded approximation and Dirichlet sets, J. Functional Analysis 6 (1970), 460–467.Google Scholar
2. Davie, A. M., Dirichlet algebras of analytic functions, J. Functional Analysis 6 (1970), 348–356.Google Scholar
3. Davie, A. M., Bounded limits of analytic functions, Proc. Amer. Math. Soc. 32 (1972), 127–133.Google Scholar
4. Gamelin, T. W., Uniform algebras, (Prentice-Hall, Englewood Cliffs, N.J., 1969).Google Scholar
5. Gamelin, T. W. and Garnett, J., Pointwise bounded approximation and Dirichlet algebras, J. Funct. Anal. 8 (1971), 360–404.Google Scholar
6. Hoffman, K., Analytic functions and logmodular Banach algebras, Acta. Math. 108 (1962), 271–317.Google Scholar
7. Savoyant, M., Thèse de Sème cycle, Montpellier (1979).Google Scholar
8. Srinivasan, and Ju-Kwei, Wang, Weak*-Dirichlet algebras, Proc. Inter. Symp. on function algebras (Tulane Univ., 1965), Scott Foresman (1966), 216–249.Google Scholar
9. Wermer, J., Seminar ilber funktionen algebren, Lecture notes in Mathematics 1 (Springer-Verlag, Berlin, 1964).Google Scholar