Hostname: page-component-669899f699-7tmb6 Total loading time: 0 Render date: 2025-04-27T12:25:31.583Z Has data issue: false hasContentIssue false
  • English
  • Français

Une formule de Riemann-Roch équivariante pour les courbes

Published online by Cambridge University Press:  20 November 2018

Niels Borne
Niels Borne*
Affiliation:
Laboratoire de Mathématiques Pures de Bordeaux, Université Bordeaux I, 351, cours de la Libération, F-33405 Talence Cedex, France courriel: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Soit 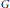$G$ un groupe fini agissant sur une courbe algébrique projective et lisse 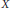$X$ sur un corps algébriquement clos $k$. Dans cet article, on donne une formule de Riemann-Roch pour la caractéristique d'Euler équivariante d'un 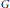$G$-faisceau inversible 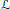$\mathcal{L}$, à valeurs dans l'anneau 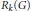${{R}_{k}}\left( G \right)$ des caractères du groupe 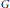$G$. La formule donnée a un bon comportement fonctoriel en ce sens qu'elle relève la formule classique le long du morphisme dim: 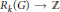${{R}_{k}}\left( G \right)\to \mathbb{Z}$, et est valable même pour une action sauvage. En guise d'application, on montre comment calculer explicitement le caractère de l'espace des sections globales d'une large classe de 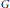$G$-faisceaux inversibles, en s'attardant sur le cas particulier délicat du faisceau des différentielles sur la courbe.

Keywords

14L3014C40group actions on varieties or schemesRiemann-Roch theorems
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 55 , Issue 4 , 01 August 2003 , pp. 693 - 710
Copyright
Copyright © Canadian Mathematical Society 2003

References

Références

[1] Benson, D. J., Representations and cohomology. I. Basic representation theory of finite groups and associative algebras. Cambridge Stud. Adv. Math. 30, Cambridge University Press, Cambridge, 1998.Google Scholar
[2] Ellingsrud, Geir and Lønsted, Knud, An equivariant Lefschetz formula for finite reductive groups. Math. Ann. 251(1980), 253–261.Google Scholar
[3] Fulton, William and Lang, Serge, Riemann-Roch algebra. Grundlehren Math. Wiss. 277, Springer-Verlag, 1985.Google Scholar
[4] Green, J. A., On the indecomposable representations of a finite group. Math. Z. 70(1958/59), 430–445.Google Scholar
[5] Grothendieck, Alexandre, Revêtements étales et groupe fondamental. SGA 1, Lecture Notes in Math. 224, Springer-Verlag, Berlin-New York, 1971.Google Scholar
[6] Grothendieck, Alexandre, Éléments de géométrie algébrique. III. Étude cohomologique des faisceaux cohérents. Inst. Hautes Études Sci. Publ. Math. 17, 1963.Google Scholar
[7] Grothendieck, Alexandre, Sur quelques points d'algègbre homologique. Tohoku Math. J. 9(1957), 119–221.Google Scholar
[8] Hartshorne, Robin, Algebraic geometry. Graduate Texts in Math. 52, Springer-Verlag, New York-Heidelberg, 1977.Google Scholar
[9] Kani, Ernst, The Galois-module structure of the space of holomorphic differentials of a curve. J. Reine Angew. Math. 367(1986), 187–206 .Google Scholar
[10] Nakajima, Shoichi, On Galois module structure of the cohomology groups of an algebraic variety. Invent. Math. 75(1984), 1–8.Google Scholar
[11] Nakajima, Shoichi, Galois module structure of cohomology groups for tamely ramified coverings of algebraic varieties. J. Number Theory 22(1986), 115–123.Google Scholar
[12] Nakajima, Shoichi, Action of an automorphism of order p on cohomology groups of an algebraic curve. J. Pure Appl. Algebra 42(1986), 85–94.Google Scholar
[13] Rzedowski-Calderón, Martha, Villa-Salvador, Gabriel and Madan, Manohar L., Galois module structure of holomorphic differentials in characteristic p. Arch. Math. (Basel) (2) 66(1996), 150–156.Google Scholar
[14] Serre, Jean-Pierre, Corps locaux. Actualités Sci. Indust. 1296, Publications de l'Institut de Mathématique de l'Universit é de Nancago VIII, Hermann, Paris, 1980.Google Scholar
[15] Serre, Jean-Pierre, Représentations linéaires des groupes finis. Hermann, Paris, 1978.Google Scholar
[16] Thomason, R. W., Algebraic K-theory of group scheme actions. In: Algebraic topology and algebraic K-theory (Princeton, NJ, 1983), Ann. of Math. Stud. 113, Princeton Univ. Press, Princeton, NJ, 1987, 539.563.Google Scholar
[17] Valentini, Robert C. and Madan, Manohar L., Automorphisms and holomorphic differentials in characteristic p. J. Number Theory 13(1981), 106–115.Google Scholar