Umbilical Submanifolds of Sⁿ × R

Abstract

We give a complete classification of umbilical submanifolds of arbitrary dimension and codimension of 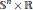${{\mathbb{S}}^{n}}\,\times \,\mathbb{R}$, extending the classification of umbilical surfaces in 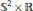${{\mathbb{S}}^{2}}\times \mathbb{R}$ by Souam and Toubiana as well as the local description of umbilical hypersurfaces in 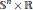${{\mathbb{S}}^{n}}\,\times \,\mathbb{R}$ by Van der Veken and Vrancken. We prove that, besides small spheres in a slice, up to isometries of the ambient space they come in a two-parameter family of rotational submanifolds whose substantial codimension is either one or two and whose profile is a curve in a totally geodesic 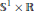${{\mathbb{S}}^{1}}\times \mathbb{R}$ or 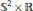${{\mathbb{S}}^{2}}\times \mathbb{R}$, respectively, the former case arising in a one-parameter family. All of them are diffeomorphic to a sphere, except for a single element that is diffeomorphic to Euclidean space. We obtain explicit parametrizations of all such submanifolds. We also study more general classes of submanifolds of 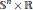${{\mathbb{S}}^{n}}\times \mathbb{R}$ and 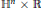${{\mathbb{H}}^{n}}\times \mathbb{R}$. In particular, we give a complete description of all submanifolds in those product spaces for which the tangent component of a unit vector field spanning the factor 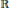$\mathbb{R}$ is an eigenvector of all shape operators. We show that surfaces with parallel mean curvature vector in 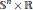${{\mathbb{S}}^{n}}\times \mathbb{R}$ and 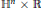${{\mathbb{H}}^{n}}\times \mathbb{R}$ having this property are rotational surfaces, and use this fact to improve some recent results by Alencar, do Carmo, and Tribuzy. We also obtain a Dajczer-type reduction of codimension theorem for submanifolds of 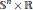${{\mathbb{S}}^{n}}\times \mathbb{R}$ and 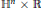${{\mathbb{H}}^{n}}\times \mathbb{R}$.