Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-12-02T23:20:36.588Z Has data issue: false hasContentIssue false
  • English
  • Français

Ultrafunctor

Published online by Cambridge University Press:  20 November 2018

Andy R. Magid
Andy R. Magid*
Affiliation:
The University of Oklahoma, Norman, Oklahoma
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let G be a functor from commutative rings to abelian groups and let ﹛Rt : i ∈ S﹜ be a family of commutative rings indexed by the set S. Let be an ultrafilter on S, and let 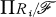denote the ultraproduct of the Rt with respect to 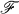. This paper studies the problem of computing from the G(Rj) via the map

The functors studied are Pic = Picard group, Br = Brauer group, U = units, and the functors K0, K1, SK1, K2 of Algebraic K-Theory. For G = Pic, U, K1 and SK1, (*) is always a monomorphism. An example is given to show that even if all the Rt are finite fields the map (*) has a kernel for G = K2.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 27 , Issue 2 , 01 April 1975 , pp. 372 - 375
Copyright
Copyright © Canadian Mathematical Society 1975

References

1. Herstein, I. N., Non commutative rings, Carus Monograph 15, Mathematical Association of America, 1968.Google Scholar
2. Milnor, J., Introduction to algebraic K-theory, Annals of Mathematics Studies 72, Princeton, 1971.Google Scholar
3. Pierce, R. S., Rings of continuous integer valued functions, Trans. Amer. Math. Soc. 100 (1961), 371–394.Google Scholar
4. Zelinsky, D., Linearly compact modules and rings, Amer. J. Math. 75 (1953), 79–90. The University of Oklahoma, Google Scholar