Hostname: page-component-6bf8c574d5-9nwgx Total loading time: 0 Render date: 2025-02-25T16:06:13.039Z Has data issue: false hasContentIssue false
  • English
  • Français

Transitivity and Ortho-Bases

Published online by Cambridge University Press:  20 November 2018

Jacob Kofner
Jacob Kofner*
Affiliation:
George Mason University, Fairfax, Virginia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Throughout this paper “space” means “T1 topological space.“

1. The concept of an ortho-base was introduced by W. F. Lindgren and P. J. Nyikos.

Definition 1. A base 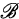of a space X is called an ortho-base provided that for each subcollection either 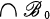is open or 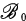is a local base of a point x ∊ X [17].

Ortho-bases are related to interior-preserving collections which have been known for some time.

Definition 2. A collection of open sets of a space X is called interior-preserving provided that the intersection of any subcollection is open. A space X is called orthocompact provided that each open cover has an open interior-preserving refinement.

It was proved in [17], in particular, that each space with an ortho-base is orthocompact, and each orthocompact developable space (which is the same as a non-archimedean quasi-metrizable developable space [4]) has an ortho-base.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 33 , Issue 6 , 01 December 1981 , pp. 1439 - 1447
Copyright
Copyright © Canadian Mathematical Society 1981

References

1. Bennett, H. R., Quasi-metrizability and the γ-space property in certain generalized ordered spaces, Topology Proceedings 4 (1979), 1–12.Google Scholar
2. Fletcher, P. and Lindgren, W. F., Transitive quasi-uniformities, J. Math. Anal. Appl. 89 (1972), 397–405.Google Scholar
3. Fletcher, P. and Lindgren, W. F., Quasi-uniformities with a transitive base. Pacific J. Math. 43 (1972), 619–631.Google Scholar
4. Fletcher, P. and Lindgren, W. F., Orthocompactness and strong Cech compactness in Moore spaces, Duke Math. J. 39 (1972), 753–766.Google Scholar
5. Fletcher, P. and Lindgren, W. F., Quasi-uniform spaces, Marcel-Dekker, to appear.Google Scholar
6. Fox, R., On metrizability and quasi-metrizability, to appear.Google Scholar
7. Fox, R., A short proof of the Junnila quasi-metrization theorem, Proc. Amer. Math. Soc, to appear.Google Scholar
8. Fox, R., Solution of the γ-space problem, Proc. Amer. Math. Soc, to appear.Google Scholar
9. Fox, R., Pretransitivity and the γ-space conjecture, to appear.Google Scholar
10. Fox, R. and Kofner, J., to appear.Google Scholar
11. Gruenhage, G., A note on quasi-metrizability, Can. J. Math. 29 (1977), 360–366.Google Scholar
12. Junnila, H., Covering properties and quasi-uniformities of topological spaces, Ph.D. thesis, Virginia Polytech. Inst, and State Univ. (1978).Google Scholar
13. Junnila, H., Neighbournets, Pacific J. Math. 76 (1978), 83–108.Google Scholar
14. Kofner, J., On A-metrizable spaces, Math. Notes 13 (1973), 168–174.Google Scholar
15. Kofner, J., Transitivity and the y-space conjecture in ordered spaces, Proc. Amer. Math. Soc., to appear.Google Scholar
16. Kofner, J., On quasi-metrizability, Topology Proceedings (1980).Google Scholar
17. Lindgren, W. F. and Nyikos, P., Spaces with bases satisfying certain order and intersection properties, Pacific J. Math. 66 (1976), 455–476.Google Scholar
18. Lindgren, W. F. and Nyikos, P., Open problems, Topology Proceedings 2 (1977), 687–688.Google Scholar