Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-13T00:46:05.841Z Has data issue: false hasContentIssue false
  • English
  • Français

Transfer of Representations and Orbital Integrals for Inner Forms of GLn

Published online by Cambridge University Press:  20 November 2018

Jonathan Cohen
Jonathan Cohen*
Affiliation:
University of Maryland, Department of Mathematics, College Park, MD 20742-4015, USA email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We characterize the Local Langlands Correspondence 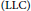$\left( \text{LLC} \right)$ for inner forms of 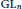$\text{G}{{\text{L}}_{n}}$ via the Jacquet–Langlands Correspondence 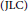$\left( \text{JLC} \right)$ and compatibility with the Langlands Classification. We show that 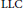$\text{LLC}$ satisfies a natural compatibility with parabolic induction and characterize 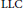$\text{LLC}$ for inner forms as a unique family of bijections 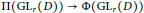$\prod \left( \text{G}{{\text{L}}_{r}}\left( D \right) \right)\,\to \,\Phi \left( \text{G}{{\text{L}}_{r}}\left( D \right) \right)$ for each $r$, (for a fixed 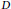$D$), satisfying certain properties. We construct a surjective map of Bernstein centers 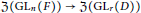$\mathfrak{Z}\left( \text{G}{{\text{L}}_{n}}\left( F \right) \right)\,\to \,\mathfrak{Z}\left( \text{G}{{\text{L}}_{r}}\left( D \right) \right)$ and show this produces pairs of matching distributions in the sense of Haines. Finally, we construct explicit Iwahori-biinvariant matching functions for unit elements in the parahoric Hecke algebras of 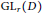$\text{G}{{\text{L}}_{r}}\left( D \right)$, and thereby produce many explicit pairs of matching functions.

Keywords

20G05Langlands correspondenceinner form
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 70 , Issue 3 , 01 June 2018 , pp. 595 - 627
Copyright
Copyright © Canadian Mathematical Society 2018

References

[1] Arthur, J. and Clozel, L., Simple algebras, base change, and the advanced theory of the trace formula. Annals of Mathematics Studies, 120, Princeton University Press, Princeton, NJ, 1989.Google Scholar
[2] Aubert, A-M., Baum, P., Plymen, R., and Solleveld, M., Geometric structure and the local Langlands conjecture. arxiv:1211.0180Google Scholar
[3] Badulescu, A., Un résultat de transfert et un résultat d'intégrabilité locale des caractères en caractéristique non nulle. J. Reine Angew. Math. 565(2003), 101–124. http://dx.doi.org/10.1515/crll.2003.096 Google Scholar
[4] Badulescu, A., Jacquet-Langlands et unitarisabilité. J. Inst. Math. Jussieu 6(2007), no. 3, 349–379. http://dx.doi.Org/10.1017/S1474748007000035 Google Scholar
[5] Bernstein, J., Deligne, P., Kazhdan, D., and Vigneras, M. F., Representations des groupes reductifs sur un corps local. Hermann, Paris, 1984.Google Scholar
[6] Borel, A., Automorphic L-functions. In: Automorphic forms, representations and L-functions (Proc. Sympos. Pure Math., Oregon State Univ., Corvallis, Ore., 1977), Part 2, Proc. Sympos. Pure Math., 33, American Mathematical Society, Providence, RI, 1979.Google Scholar
[7] Carter, R., Finite groups of Lie type: Conjugacy classes and complex characters. Reprint of the 1985 original, John Wiley & Sons, Ltd., Chichester, 1993.Google Scholar
[8] Deligne, P. and Lusztig, G., Representations of reductive groups over finite fields. Ann. of Math. 103(1976), no. 1, 103–161. http://dx.doi.org/10.2307/1971021 Google Scholar
[9] Haines, T. J., The stable Bernstein center and test functions for Shimura varieties. In: Automorphic forms and Galois representations, 2, London Math. Soc. Lecture Note Ser., 415, Cambridge University Press, Cambridge, 2014, pp. 118–86.Google Scholar
[10] Haines, T. J., On Satake parameters for representations with parahoric fixed vectors. Int. Math. Res. Not. IMRN 2015, no. 20, 10367–10398. http://dx.doi.org/10.1093/imrn/rnu254Google Scholar
[11] Henniart, G., Une caractérisation de la correspondance de Langlands locale pour GL(n). Bull. Soc. Math. France 130(2002), no. 4, 587–602. http://dx.doi.org/10.24033/bsmf.2431 Google Scholar
[12] Jacquet, H., Piatetskii-Shapiro, I. I., and Shalika, J. A., Rankin-Selberg convolutions. Amer. J. Math. 105(1983), no. 2, 367–464. http://dx.doi.org/10.2307/2374264 Google Scholar
[13] Kazhdan, D., Cuspidal geometry of p-adic groups. J. Analyse Math. 47(1986), 1–36. http://dx.doi.org/10.1007/BF02792530 Google Scholar
[14] Kazhdan, D., Representations of groups over close local fields. J. Analyse Math. 47(1986), 175–179. http://dx.doi.org/10.1007/BF02792537 Google Scholar
[15] Kazhdan, D. and Varshavsky, Y., On endoscopic transfer of Deligne-Lusztig functions. Duke Math. J. 161(2012), no. 4, 675–732. http://dx.doi.org/10.1215/00127094-1548371 Google Scholar
[16] Kottwitz, R., Sign changes in harmonic analysis on reductive groups. Trans. Amer. Math. Soc. 278(1983), no. 1, 289–297. http://dx.doi.org/10.1090/S0002-9947-1983-0697075-6 Google Scholar
[17] Kottwitz, R., Shimura varieties and twisted orbital integrals. Math. Ann. 269(1984), no. 3, 287–300. http://dx.doi.Org/10.1007/BF01450697 Google Scholar
[18] Kottwitz, R., Tamagawa numbers. Ann. of Math. (2) 127(1988), no. 3, 629–646. http://dx.doi.org/10.2307/2007007 Google Scholar
[19] Laumon, G., Cohomology of Drinfeld modular varieties. Part 1: Geometry, counting of points and local harmonic analysis. Cambridge Studies in Advanced Mathematics, 41, Cambridge University Press, Cambridge, 1996.Google Scholar
[20] Raghuram, A., On representations of p-adic GL2(D). Pacific J. Math. 206(2002), no. 2, 451–464. http://dx.doi.Org/10.2140/pjm.2002.206.451 Google Scholar
[21] Roche, A., The Bernstein decomposition and the Bernstein centre. In: Ottawa lectures on admissible representations of reductive p-adic groups, Fields Inst. Monogr., 26, American Mathematical Society, Providence, RI, 2009, pp. 3–52.Google Scholar
[22] Scholze, P., The Langlands-Kottwitz approach for the modular curve. Int. Math. Res. Not. IMRN 2011, no. 15, 3368–3425. http://dx.doi.org/10.1093/imrn/rnq225 Google Scholar
[23] Scholze, P., The local Langlands correspondence for GL(n) over p-adic fields. Invent. Math. 192(2013), no. 3, 663–715. http://dx.doi.org/10.1007/s00222-012-0420-5 Google Scholar
[24] Tadić, M., Induced representation of GL(n, A) for p-adic division algebras A. J. Reine Angew. Math. 405(1990), :48–77. http://dx.doi.org/10.1515/crll.1990.405.48 Google Scholar
[25] Zelevinsky, A. V., Induced representations of reductive p-adic groups. II. On irreducible representations of GL(n). Ann. Sci. Ecole Norm. Sup. (4) 13(1980), no 2, 165–210. http://dx.doi.Org/10.24033/asens.1379 Google Scholar