Hostname: page-component-745bb68f8f-s22k5 Total loading time: 0 Render date: 2025-02-03T07:33:21.396Z Has data issue: false hasContentIssue false
  • English
  • Français

Transcendental Elements in Continuous Rings

Published online by Cambridge University Press:  20 November 2018

Israel Halperin
Israel Halperin*
Affiliation:
Queen's University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In (2), John von Neumann introduced the concept of a continuous ring 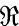as a generalization to the infinite limiting case of the total matric algebras over a division ring. Von Neumann sketched a theory of arithmetic for such continuous rings 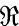and asserted :

(⋆) every continuous ring 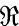contains purely transcendental elements c.

This means: for every polynomial p(t) = tm + Z1tm-1 + . . . + zm {m ≥ 1) which has all coefficients zi in the centre of 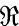, the element p(c) has a reciprocal in 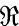, that is, (p(c))-l exists such that p(c).(p(c))-l = (p(c))-l.p(c) = 1.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 14 , 1962 , pp. 39 - 44
Copyright
Copyright © Canadian Mathematical Society 1962

References

1. Halperin, Israel, Van Neumann's Arithmetics of Continuous Riugs, Acta Sci. Math. Szeged, to appear.Google Scholar
2. von Neumann, J., Continuous rings and their arithmetics, Proc. Nat. Acad. Sci. (U.S.A.), 23 (1937), 341–349.Google Scholar
3. von Neumann, J., Continuous geometry, Parts I, II, III (Princeton: Princeton University Press, 1960).Google Scholar